poomocyyyyyyyyy hejhej: Przez punkt (−1, 1) poprowadzono prosta tak, aby srodek jej odcinka zawartego miedzy prostymi x + 2y = 1 i x + 2y = 3 nalezał do prostej x − y = 1. Wyznaczyc równanie symetralnej odcinka.

hejhej:

	1		1
czy a= −		a b=
	2		2

Tadeusz: to zadanie było kilka/kilkanaście dni temu. Zrób rysunek i baw się −

hejhej: ale wlasnie nie wiem co i jak...

hejhej: prosze ludziska...

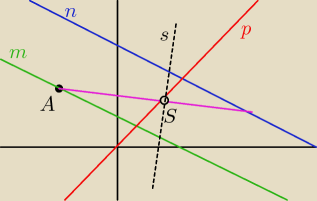
Tadeusz: szukasz równania prostej s

hejhej: a skad te linie wszystkie?

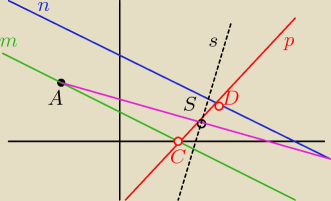
Tadeusz: SPAPRAŁEM RYSUNEK 1. zauważ, że punkt A=(−1,1) leży na prostej m: x+2y=1 ... bo spełnia jej równanie 2. poszukaj punktów przecięcia się prostych m i p oraz n i p (nie zaznaczyłem ich na rys.) Zaznacz je jako C i D. Powinno Ci wyjść C=(0,1) i D=(5/3, 2/3)

Tadeusz: m: x+2y=1 n: x+2y=3 p: x−y=1 A=(−1,1) ... to Twoje warunki zadania

Tadeusz: dalej: Punkt S wyznaczysz jako środek odcinka CD S=(4/3, 1/3) Piszesz równanie prostej przechodzącej przez punkty A i S a potem równanie symetralnej −