Geometria analityczna.
KrysteK: Punkty A = (7,1) i C = (1,3) są przeciwległymi wierzchołkami trapezu równoramiennego ABCD.
Prosta l o równaniu y=x jest osią symetrii trapezu.
a) Oblicz pole trapezu.
b) Napisz równanie okręgu opisanego na tym trapezie.
3 lis 18:20
dero2005:
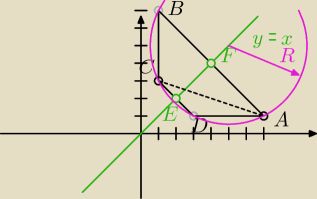
1) oblicz równanie prostej AF
a
AF = −1
y
AF = a
AF(x − x
A) + y
A = −1(x−7)+1 = −x + 8
porównujemy równania y = −x + 8 i y = x i znajdujemy punkt F
−x + 8 = x
x = 4 y = 4
F = (4 , 4)
2) oblicz równanie prostej CE
a
CE = −1
y
CE = a
CE(x − x
C) + y
C = −1(x − 1) + 3 = −x + 4
porównujemy równania y
CE = −x + 4 i y = x i znajdujemy punkt E
−x + 4 = x
x = 2 y = 2
E= (2 , 2)
3) oblicz odległość punktów EF ( wysokość trapezu)
|EF| =
√(xF−xE)2+(yF−yE)2 =
√(4−2)2+(4−2)2 =
√4+4 =
√8 = 2
√2
4) oblicz odległość punktów AF
|AF| =
√(xA−xF)2+(yA−yF)2 =
√(7−4)2+(1−4)2 =
√9+9 =
√18 = 3
√2
5) oblicz odległość punktów CE
|CE| =
√(xC−xE)2+(yC−yE)2 =
√(1−2)2+(3−2)2 =
√1+1 =
√2
6) oblicz pole trapezu
P = (|AF| + |CE|)*|FE| = (3
√2+
√2)*2
√2 = 4
√2*2
√2 = 16 [j
2]
7) oblicz promień okręgu opisany na trapezie R
trzeba go liczyć jako promień okręgu opisanego na trójkącie ABC lub ADC
trzeba wykorzystać wzory
| | abc | | a | | b | | c | |
R = |
| i |
| = |
| = |
|
|
| | 4PΔ | | sinα | | sinβ | | sinγ | |
gdzie a, b, c długości boków poszczególnych trójkatów, P
Δ − pole trójkątów
3 lis 21:27
Gustlik: Ja mam taki pomysł:
Najpierw sposobem
dero2005 znajduję współrzędne punktów E i F.
Mam teraz dane:
A=(7, 1)
C=(1, 3)
E=(2, 2)
F=(4, 4)
Obliczam współrzędne B.
Liczę współrzędne wektora AF
→
AF
→=[4−7, 4−1]=[−3, 3]
AF
→=FB
→=[−3, 3]
FB
→=[x
B−4, y
B−4]
x
B−4=−3, y
B−4=3
x
B=1, y
B=7
B=(1, 7)
Obliczam współrzędne D.
Liczę współrzędne wektora CE
→
CE
→=[2−1, 2−3]=[1, −1]
ED
→=CE
→=[1, −1]
ED
→=[x
D−2, y
D−2]
x
D−2=1, y
D−2=−1
x
D=3, y
D=1
D=(3, 1)
Mam dane wszystkie wierzchołki trapezu:
A=(7, 1)
B=(1, 7)
C=(1, 3)
D=(3, 1)
Liczę współrzędne wektorów AB
→, AC
→, AD
→
AB
→=[1−7, 7−1]=[−6, 6]
AC
→=[1−7, 3−1]=[−6, 2]
AD
→=[3−7, 1−1]=[−4, 0]
Liczę pole ΔABC z wyznacznika wektorów:
d(AB
→, AC
→)=
| −6 6 |
| −6, 2 |
=−6*2−6*(−6)=−12+36=24
| | 1 | |
PΔABC= |
| |d(AB→, AC→)|=12
|
| | 2 | |
Liczę pole ΔACD z wyznacznika wektorów:
d(AC
→, AD
→)=
| −6 2 |
| −4, 0 |
=−6*0−2*(−4)=0+8=8
| | 1 | |
PΔACD= |
| |d(AC→, AD→)|=4
|
| | 2 | |
P
trapezu=P
ΔABC+P
ΔACD=12+4=16
Ciąg dalszy jak u
dero2005 pkt. 7.
Obliczamy promień wg wskazówek
dero2005 − wybieramy trójkąt ABC lub ACD, wyznaczamy
równanie symetralnej jednego z boków trójkąta (ale innej niż prosta EF będąca symetralną boków
AB i CD), wyznaczamy równanie prostej EF i tej drugiej symetralnej i układem równań wyznaczamy
punkt przecięcia symetralnych − będzie to srodek okręgu.
4 lis 00:32
KrysteK: Dzięki wielkie!

5 lis 08:35
nika9518: dero2005:
"aAF = −1 "
skąd to bierzemy? takze robie to zadanie ale nie mam pojęcia skąd to −1
5 sty 17:34
dero2005:
"prosta y = x jest osią symetrii trapezu" czyli jest prostopadła do podstawy trapezu, ponieważ
współczynnik "a" prostej y = x wynosi 1 to współczynnik prostej zawierającej podstawę
(prostopadłej) wynosi −1
5 sty 20:51
 1) oblicz równanie prostej AF
aAF = −1
yAF = aAF(x − xA) + yA = −1(x−7)+1 = −x + 8
porównujemy równania y = −x + 8 i y = x i znajdujemy punkt F
−x + 8 = x
x = 4 y = 4
F = (4 , 4)
2) oblicz równanie prostej CE
aCE = −1
yCE = aCE(x − xC) + yC = −1(x − 1) + 3 = −x + 4
porównujemy równania yCE = −x + 4 i y = x i znajdujemy punkt E
−x + 4 = x
x = 2 y = 2
E= (2 , 2)
3) oblicz odległość punktów EF ( wysokość trapezu)
|EF| = √(xF−xE)2+(yF−yE)2 = √(4−2)2+(4−2)2 = √4+4 = √8 = 2√2
4) oblicz odległość punktów AF
|AF| = √(xA−xF)2+(yA−yF)2 = √(7−4)2+(1−4)2 = √9+9 = √18 = 3√2
5) oblicz odległość punktów CE
|CE| = √(xC−xE)2+(yC−yE)2 = √(1−2)2+(3−2)2 = √1+1 = √2
6) oblicz pole trapezu
P = (|AF| + |CE|)*|FE| = (3√2+√2)*2√2 = 4√2*2√2 = 16 [j2]
7) oblicz promień okręgu opisany na trapezie R
trzeba go liczyć jako promień okręgu opisanego na trójkącie ABC lub ADC
trzeba wykorzystać wzory
1) oblicz równanie prostej AF
aAF = −1
yAF = aAF(x − xA) + yA = −1(x−7)+1 = −x + 8
porównujemy równania y = −x + 8 i y = x i znajdujemy punkt F
−x + 8 = x
x = 4 y = 4
F = (4 , 4)
2) oblicz równanie prostej CE
aCE = −1
yCE = aCE(x − xC) + yC = −1(x − 1) + 3 = −x + 4
porównujemy równania yCE = −x + 4 i y = x i znajdujemy punkt E
−x + 4 = x
x = 2 y = 2
E= (2 , 2)
3) oblicz odległość punktów EF ( wysokość trapezu)
|EF| = √(xF−xE)2+(yF−yE)2 = √(4−2)2+(4−2)2 = √4+4 = √8 = 2√2
4) oblicz odległość punktów AF
|AF| = √(xA−xF)2+(yA−yF)2 = √(7−4)2+(1−4)2 = √9+9 = √18 = 3√2
5) oblicz odległość punktów CE
|CE| = √(xC−xE)2+(yC−yE)2 = √(1−2)2+(3−2)2 = √1+1 = √2
6) oblicz pole trapezu
P = (|AF| + |CE|)*|FE| = (3√2+√2)*2√2 = 4√2*2√2 = 16 [j2]
7) oblicz promień okręgu opisany na trapezie R
trzeba go liczyć jako promień okręgu opisanego na trójkącie ABC lub ADC
trzeba wykorzystać wzory
