bardzo proszę o pomoc K: znajdź cosinus kąta pomiędzy obrazami boków AB i BC trójkąta ABC przez powinowactwo prostokątne o skali k=4 względem prostej x=3 jeśli A=(2,1) B=(4,5) i C=(−2,3)

K: czyli najpierw każdy punkt przekształcam przez to powinowactwo czy całe odcinki?

K: czy ktoś wie?

hwdtel i det 0: Dane powinowactwo prostokątne przekształci Δ_ABC w Δ_A'B'C' taki,że → → A'(−4:1) , B'(4:5) , C'(−20:3) A zatem :B'A'(8;4) B'C'(24;2)

	B'A'oB'C'		8*24 + 4*2
cos∡(B'A';B'C') =		=
	|B'A'||B'C'|		(√82+42)(√242+22)

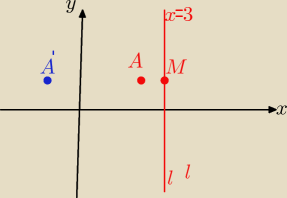Aga: Powinowactwo prostokątne o osi l i skali k≠0 to przekształcenie, w którym obrazem punktu A jest A' taki, że wektor MA'=k* wektor MA M−rzut prostokątny Punktu A na oś l. A(2;1) M(3,1) k=4 , A'(x';y') wektor MA'=[x'−3;y'−1] k*wektor MA=4*[−1;0]=[−4;0] x'−3=−4 i y'−1=0 z równości wektorów. stąd x'=−1, y'=1, czyli A'=(−1,1) podobny sposób znajdź punkty B' i C'. Znajdź długości boków trójkąta A'B'C' i wykorzystaj twierdzenie cosinusów.