Sporzadzenie wykresu funkcj i podanie jej wlasnosci Piotr: Witam, mam problem z takim oto zadaniem: sporządzic wykresu funkcji f:x→R i podać jej własności, gdzie: i mam trzy przykłady: a) f(x)=max(x,x2) , X=R, b) f(x)=min (x,x3) , X=R c) f(x)=L2x (zamknięte jest to takim samym znakiem jak przed 2 tylko odwróconym, nie mam pewności czy to jest nawias kwadratowy czy bazgroły mojego wykładowcy : \ ) narysować przykład a potrafię, ale nie umiem podać własności, proszę o pomoc oraz wyjaśnienie... chciałbym to zrozumieć .

Daromir: Otóż przykład b) jest podobny do narysowania jak a), tylko bierzesz tą mniejszą liczbę. W przypadku c) twojemu wykładowcy pewnie chodziło o funkcję "część całkowita", czyli największą liczbę całkowitą c, która nie jest większa od x.(tutaj 2x) Jeśli chodzi o własności, to możesz podać miejsca zerowe ( w a 0), przedziały monotoniczności ( w a f rośnie dla liczb dodatnich, maleje dla ujemnych), możesz podać dziedzinę i zbiór wartości, czy funkcja jest parzysta/nieparzysta, czy jest różnowartościowa...

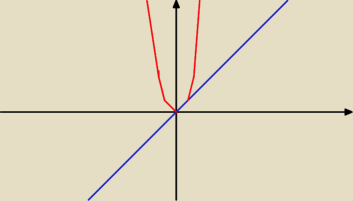
Piotr: a wiec wykresy powinny wyglądać tak : to dla przykładu a

Piotr: tu przykład b

Piotr: a c powinno wygladac tak ? https://matematykaszkolna.pl/strona/979.html

Daromir: Nie bardzo wiem dlaczego zostawiłeś obie figury na rysunku. To nawet nie jest funkcja. W przykładzie a na wykresie zostaje tylko to, co jest większe dla danego x, w b tylko to co jest mniejsze. c wygląda podobnie, tylko jest "rozciągnięte" (argumentem jest 2x).

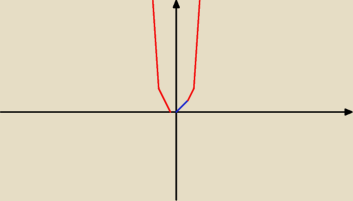
Piotr: a chyba już rozumiem czyli a powinno wyglądać tak :

Daromir: Dokładnie

sushi_ gg6397228: masz parabole a na odcinku (0,1) masz kawałek prostej

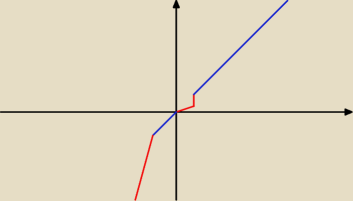
Piotr: a b) tak :

Daromir: Zgadza się

Piotr: a teraz własności: dla a będzie to tak wyglądać ? miejsce zerowe: x=0 monotoniczność: funkcja jest przedziałami monotoniczna rosnąca w przedziale (−∞, −1> dziedzina: D = R zbiór: ZW = R parzystość: funkcja nie jest ani parzysta ani nieparzysta

Daromir: Czy na pewno mówisz o przykładzie a)? funkcja jest malejąca w przedziale (−∞, 0) rosnąca w (0; +∞). Zbiorem wartości jest [0;+∞) R możesz przyjąć jako przeciwdziedzinę, nie jednak jako zbiór wartości.

Piotr: miałem na myśli przykład a), ale chyba porąbalo mi sie totalnie dopiero się uczę tego diabelstwa wiec i mogę błędy popełniać chyba już widzę jak powinno być w a) to teraz b) (dla sprawdzenia czy załapałem) miejsce zerowe: x=0 monotoniczność: funkcja jest przedziałami monotoniczna malejąca (−∞, 0> rosnąca <0, +∞) dziedzina: D= −∞;+∞ zbiór: −∞;+∞ parzystość: funkcja nie jest ani parzysta ani nieparzysta

Daromir: Wszystko ok, ale funkcja jest rosnąca w całej dziedzinie

Piotr: ok super wielkie dzięki uratowałeś mi życie

Piotr: a Jeszce co do przykładu c) to własność tak będzie wyglądać : ? https://matematykaszkolna.pl/strona/979.html miejsce zerowe: x=0 monotoniczność: (w tym wypadku nie mam pojęcia :\ ) dziedzina: D= R zbiór: (−6,−5¹₄) (−4,−3¹₃) (−2,−1¹₂) (0,0) (4,3¹₃) (4,3¹₃) (6,5¹₄) parzystość: funkcja nie jest ani parzysta ani nieparzysta