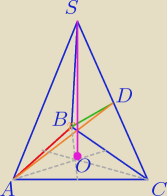
 Ostrosłup prawidłowy trójkątny o wysokości 2a i krawędzi podstawy a przecięto płaszczyzną
przechodzącą przez krawędź AB podstawy ostrosłupa i przez środek D przeciwległej krawędzi
bocznej CS. Wyznacz pole otrzymanego przekroju.
zacznę wpierw od rysunku, poprawny? (przekrój to ten trójkąt o kolorach: zielony, czerwony,
pomarańczowy, aby się lepiej wyróżniał)
Ostrosłup prawidłowy trójkątny o wysokości 2a i krawędzi podstawy a przecięto płaszczyzną
przechodzącą przez krawędź AB podstawy ostrosłupa i przez środek D przeciwległej krawędzi
bocznej CS. Wyznacz pole otrzymanego przekroju.
zacznę wpierw od rysunku, poprawny? (przekrój to ten trójkąt o kolorach: zielony, czerwony,
pomarańczowy, aby się lepiej wyróżniał)
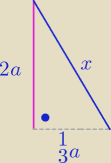 Skoro:
H = 2a
Ostrosłup prawidłowy to w podstawie trójkąt równoboczny, więc mogę obliczyć wysokość w
trójkącie ASC itp.
Zatem: (x∊R+)
Skoro:
H = 2a
Ostrosłup prawidłowy to w podstawie trójkąt równoboczny, więc mogę obliczyć wysokość w
trójkącie ASC itp.
Zatem: (x∊R+)
| 1 | ||
4a2 + | a2 = x2 | |
| 9 |
| 36a2 | a2 | ||
+ | = x2 | ||
| 9 | 9 |
| 40a2 | ||
x2 = | ||
| 9 |
| 2√10a | ||
x = | ||
| 3 |
| 1 | ||
x2 = 4a2 + | a2 | |
| 9 |
| 36a2 | a2 | |||
x2 = | + | |||
| 9 | 9 |
| 37a2 | ||
x2 = | ||
| 9 |
| √37a | ||
x = | ||
| 3 |
| √39a | ||
No teraz jakoś ładniej wyszło tylko w książce podane jest: x = | więc gdzie jest | |
| 3 |
 <załamka> Zaraz naprawie
<załamka> Zaraz naprawie 
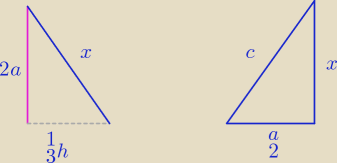
| 1 | 1 | |||
Po pierwsze zrobiłem błąd w tym, że nie jest | a tylko | h  , natomiast h = , natomiast h = | ||
| 3 | 3 |
| a√3 | ||
 | ||
| 2 |
| 1 | a√3 | a√3 | |||
* | = | ||||
| 3 | 2 | 6 |
| 3a2 | ||
x2 = 4a2 + | ||
| 36 |
| 144a2 | 3a2 | |||
x2 = | + | |||
| 36 | 36 |
| 147a2 | ||
x2 = | ||
| 36 |
| √147a | ||
x = | ||
| 6 |
| a | ||
x2 + ( | )2 = c2 | |
| 2 |
| 147a2 | a2 | ||
+ | = c2 | ||
| 36 | 4 |
| 147a2 | 9a2 | ||
+ | = c2 | ||
| 36 | 36 |
| 156a2 | |
= c2 | |
| 36 |
| √156a | 2√39a | √39a | ||||
c = | = | = | ||||
| 6 | 6 | 3 |

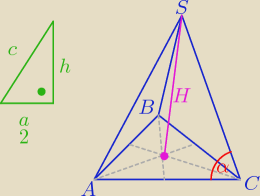 Kolejny element według mnie to obliczenie cosα w trójkącie między wysokością ściany bocznej
itp.
Zatem:
Kolejny element według mnie to obliczenie cosα w trójkącie między wysokością ściany bocznej
itp.
Zatem:
| ||||||||
cosα = | ||||||||
| c |
| a | 3 | 3a | |||||||||||
cosα = | = | * | = | = | ||||||||||
| 2 | √39a | 2√39a |
| 3 | √39 | 3√39 | √39 | |||||
= | * | = | = | |||||
| 2√39 | √39 | 78 | 26 |
 . Zabieram się za inne zadanie.
. Zabieram się za inne zadanie.

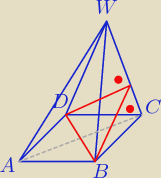 Wiem, że jest to kąt dwuścienny. Więc chyba rysunek dobrze
Wiem, że jest to kąt dwuścienny. Więc chyba rysunek dobrze 
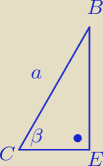 W sumie zadanko jest bardzo proste
W sumie zadanko jest bardzo proste  , mianowicie:
, mianowicie:
| |BE| | ||
sinβ = | / * a | |
| a |
