w trójkącie ABC wierzchołki mają współrzędne A(-7,-1); B(-1,-3); C (-5,-1) a) sp
paulka: w trójkącie ABC wierzchołki mają współrzędne A(−7,−1); B(−1,−3); C (−5,−1)
a) sprawdź że trójkąt jest prostokątny
b) oblicz pole trójkąta ABC
c) wyznacz równanie okręgu opisanego na tym trójkącie
31 paź 18:29
dero2005:
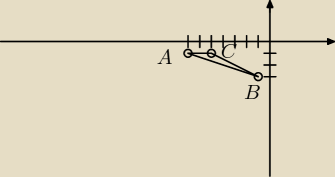
|AB| =
√(xB−xA)2 + yB−yA)2 =
√(−1+7)2 + (−3+1)2 =
=
√62 + (−2)2 =
√36+4 =
√40 = 2
√10
|BC| =
√(xC−xB)2 + (yC−yB)2 =
√(−5+1)2 + (−1+3)2 =
=
√(−4)2 + 22 =
√16 + 4 =
√20 = 2
√5
|AC| =
√(xC−xA)2 + (yC−yA)2 =
√(−5+7)2 + (−1+1)2 =
=
√22 + 02 =
√4+0 =
√4 = 2
(|AC|)
+ (|BC|)
2 = (|AB|)
2
2
2 + (2
√5)
2 = (2
√10)
2
4 + 20 ≠ 40
24 ≠ 40 nie jest prostokątny
pole
P =
12|det(AC,AB)|
AC→ = [(−5−(−7)) , −1 −(−1)] = [2 , 0]
AB→ = [(−1−(−7)) , −3−(−1)] = [6 , −2]
det|(AC→,AB→)| = |2*(−2) − 6*0| = |−4| = 4
P =
42 = 2
| | |AB|*|AC|*|BC| | |
R = |
| = 5√10 |
| | 8 | |
31 paź 21:05
beataa: dane sa dwa wierzchołki A(1,2) i B (5,2) trójkata równobocznego ABC.
a) oblicz pole trójkąta ABC
b)wyznacz współrzędne wierzchołka C tego trójkąta
28 paź 12:44
Janek191:
→
AB = [ 4, 0 ] ⇒ a = I AB I = 4
a)
28 paź 13:02
Janek191:
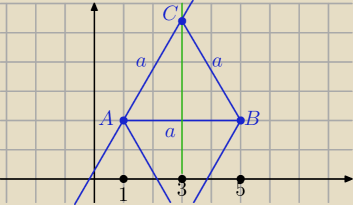
C = ( 3, y)
y = 2 + 2
√3
C = ( 3, 2 + 2
√3) lub C = ( 3, 2
√3 − 2)
28 paź 13:12
Janek191:
Poprawka

C = ( 3 , 2 + 2
√3 ) lub C = ( 3, 2 − 2
√3)
28 paź 13:13
Mariusz:
A(−7,−1); B(−1,−3); C (−5,−1)
AB=[6,−2] BC=[−4,2]
6*(−4)−(−2)*2=−24−(−4)=−20<0 // Tutaj liczymy przeskalowanego cosinusa między wektorami AB i BC
kąt między AB i BC jest rozwarty więc trójkąt nie może być prostokątny
28 paź 22:07
 |AB| = √(xB−xA)2 + yB−yA)2 = √(−1+7)2 + (−3+1)2 =
= √62 + (−2)2 = √36+4 = √40 = 2√10
|BC| = √(xC−xB)2 + (yC−yB)2 = √(−5+1)2 + (−1+3)2 =
= √(−4)2 + 22 = √16 + 4 = √20 = 2√5
|AC| = √(xC−xA)2 + (yC−yA)2 = √(−5+7)2 + (−1+1)2 =
= √22 + 02 = √4+0 = √4 = 2
(|AC|) + (|BC|)2 = (|AB|)2
22 + (2√5)2 = (2√10)2
4 + 20 ≠ 40
24 ≠ 40 nie jest prostokątny
pole
P = 12|det(AC,AB)|
AC→ = [(−5−(−7)) , −1 −(−1)] = [2 , 0]
AB→ = [(−1−(−7)) , −3−(−1)] = [6 , −2]
det|(AC→,AB→)| = |2*(−2) − 6*0| = |−4| = 4
P = 42 = 2
|AB| = √(xB−xA)2 + yB−yA)2 = √(−1+7)2 + (−3+1)2 =
= √62 + (−2)2 = √36+4 = √40 = 2√10
|BC| = √(xC−xB)2 + (yC−yB)2 = √(−5+1)2 + (−1+3)2 =
= √(−4)2 + 22 = √16 + 4 = √20 = 2√5
|AC| = √(xC−xA)2 + (yC−yA)2 = √(−5+7)2 + (−1+1)2 =
= √22 + 02 = √4+0 = √4 = 2
(|AC|) + (|BC|)2 = (|AB|)2
22 + (2√5)2 = (2√10)2
4 + 20 ≠ 40
24 ≠ 40 nie jest prostokątny
pole
P = 12|det(AC,AB)|
AC→ = [(−5−(−7)) , −1 −(−1)] = [2 , 0]
AB→ = [(−1−(−7)) , −3−(−1)] = [6 , −2]
det|(AC→,AB→)| = |2*(−2) − 6*0| = |−4| = 4
P = 42 = 2

 C = ( 3 , 2 + 2√3 ) lub C = ( 3, 2 − 2√3)
C = ( 3 , 2 + 2√3 ) lub C = ( 3, 2 − 2√3)