prawdopodobieństwo Jacek: sushi gg6397228, Basia, Eta moglibyście mi wytłumaczyć to: 1. "W urnie są kule: 4 białe, 5 czarnych i 3 zielone. Wylosowano trzy razy po jednej kuli, bez zwracania. Oblicz prawdopodobieństwo, że wylosowano kule w różnych kolorach" 2. "W urnie jest 5 kul białych i n czarnych. Wylosowano dwie kule bez zwracania.

	15
Prawdopodobieństwo wylosowania kuli białej i czarnej jest nie mniejsze od		. Wyznacz
	28

liczbę n". Pytanie polega na tym: dlaczego zadanie 1 zrobione jest wariacją bez powtórzeń, a drugie kombinacją? Od czego to zależy, ponieważ drugie również zrobiłbym to wariacją ale wyjdzie inny wynik. Drugie pytanie odnośnie zadania 1: zdanie sprzyjające to |A| = 3! * 3 * 4 * 5. Pytanie: skąd ta 3!? bo 3 * 4 * 5 <− to chyba te rózne liczby, ale czemu silnia tam tez jest to nie wiem

sushi_ gg6397228: ad 1 bo moga byc rozne kolejnosci wylosowania kulek b,c,z b,z,c z,b,c z,c,b c,z,b c,b,z masz 6 mozliwosci−−−> 3!

sushi_ gg6397228: ad 2 mamy miec czarna i biala oraz wylosowano dwie kule bez zwracania−−> wsadzono reke i od razu są dwie kulki−−> wiec nie ma znaczenia kolejnosc kul w reku−−> chcemy aby byly roznych kolorow

Jacek: Czyli tak naprawdę w zadaniu trzeba zauważyć słówko "wylosowano trzy razy po jednej kuli" to jest kluczowe tak?

Jacek: I mam jeszcze jedno pytanie: https://matematykaszkolna.pl/forum/107880.html czy tutaj to co podała Basia na pewno dobrze jest chodzi mi o tę "4". Bo nie jest zgodne z odpowiedziami

sushi_ gg6397228: to mowi wtedy o wariancjach, a nie kombinacjach a potem trzeba ustawiac kolejnosci (rozpatrzec warianty) np wylosowano 2 biale b,b, z 4*3* 3 b,b,c 4*3* 5 z,b,b 3*4*3 c,b,b 5*4*3 b,z,b 4*3*3 b,c,b 4*5*3 czyli znowu by bylo 6 mozliwosci

sushi_ gg6397228: z,b,b,b b,z,b,b b,b,z,b b,b,b,z masz mozliwosc ulokowania kul bialych 4− mozliwosci

Jacek: Ok bardzo dziękuje za wytłumaczenie tego Jednak zacząłem wczoraj inny typ zadań z prawdopodobieństwa, mianowicie z drzewkami. Mógłbyś tak wyjaśnić o co mniej więcej chodzi na podstawie tego zadania: "W urnie jest 6 kul bialych i n czarnych. Dwie losowo wybrane kule przekładamy do drugiej początkowo pustej urny. Wiedząc, że prawdopodobieństwo wylosowania teraz z drugiej urny kuli

	4
białej jest większe od		wyznacz liczbę n"
	5

Od czego w ogóle zacząć rysowanie takich drzewek ?

sushi_ gg6397228: drzewka to sie rysuje podzial (np, orzel, reszka ; biale , czarne, niebieskie; biale , pozostale kolory) w zadaniu robisz najpierw podzial biale i czarne

Jacek: Po tym zadaniu co podesłałem z tym "*4" mam wątpliwości co do innego zadania, mianowicie: "W skrzynce znajduje się 50 identycznych żarówek, wśród których 5 jest wadliwych.Kupujemy 4 żarówki. Oblicz prawdopodobieństwo, że wsród żarówek jedna jest wadliwa." To

	50 5
|Ω| =

I teraz znowu wątpliwość: Moje:

	5 1		45 3
|A| =		*		* 4

Rozwiązanie:

	5 1		45 3
|A| =		*

Czemu tutaj w rozwiązaniu nie mnoży się przez ułożeine? Ilość przypadków?

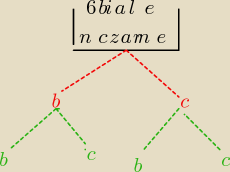
sushi_ gg6397228: na kazdej gałęzi piszesz jakie jest prawdopodobienstwo

ilosc kul danego koloru
wszystkie kule w pudelku

sushi_ gg6397228: bo mamy miec wadliwa zarowke, wiec nas nie interesuje na ktorym miejscu bedzie wylosowana poza tym−−> daleś moc omega== kombinacje−−−> wiec wtedy tez zbior A musi miec kombinacje jezeli dasz Ω= wariancje to wtedy zbior A domnozysz na kolejnosc

Jacek: Aha czyli przy: 1^o Kombinacjach nie mnożymy przez ilość przypadków 2^o Wariacjach mnożymy przez ilość przypadków, tak?

sushi_ gg6397228: zgadza sie kombinacje−−> kolejnosc nie istotna−−> wybor kart, wybor do druzyny, do reprezentacji, totolotek(tylko 20 z 80 czy 6 z 49; bez szczesliwych numerkow)−−> wazne aby byc w druzynie wariacje + permutacje −−> kolejnosc wazna −−> stanie w kolejce, numer pin, liczby

Jacek: Dziękuje bardzo dzięki temu właśnie zrozumiałem zadania z prawdopodobieństwa których przedtem nie rozumialem. To teraz pozostały te drzewka nieszczęsne

sushi_ gg6397228: drzewka sa bardzo łatwe−−> bo zawsze sie mnozy po danych galeziach w dól i na dole wybiera odpowiednie warunki zrob sobie takie zadanko: 3 razy rzut moneta−−> P(A)= wypadł dwa razy orzel