objętość walca jarke: objętość walca + ciąg geometryczny Przekroje osiowe pięciu walców są kwadratami których pola w cm² są kolejnymi wyrazami ciągu geometrycznego o ilorazie ¹₄, a suma pól tych kwadratów jest równa 5²¹₆₄ cm². Oblicz objętość najmniejszego walca. Nie proszę o rozwiązanie, tylko o wskazówki. Z góry dziękuję.

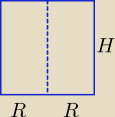
Bogdan: H − wysokość najmniejszego walca, R − długość promienia najmniejszego walca. Najmniejszy kwadrat ma pole H², każdy następny kwadrat ma pole 4 razy większe od poprzedniego. Pola tworzą więc ciąg geometryczny o ilorazie q = 4 (to nie pomyłka, dla wygody obliczeń odwróciłem monotoniczność ciągu).

	45 − 1		341
Suma pięciu wyrazów tego ciągu: S5 = H2*		i S5 =
	4 − 1		64

Czy już wiesz, co robić dalej?

jarke: Tak, rozwiązałem już dalszą część. Rysunku mi brakowało, podstawa to 2R, u mnie wynosiła R i dlatego nie wychodziło, nie wiem jak mogłem to pomylić i myślałem, że H nie wynosi jednak

	1
	8

dzięki Bogdan

Agusia: Mam pytanie , jeżeli ja w tym zadaniu wzięłam q=1/4 to i tak powinno mi wyjść dobry wynik a tak niesttey nie jest. Czy może mi ktoś wytłumaczyć dlaczego i o co chodzi z tą zamiana q=1/4 na q=4 że wzór się zmienił może nie wzór ale zapis.....

pigor: ... no to "po bożemu" : niech 2r − długość boku kwadratu , to z warunków zadania : ciąg pól przekrojów osiowych walca (a_n)= (4r², r²,¹₄r² , ...) , gdzie n=5, q=¹₄, a₁=4r² , S₅=³⁴¹₆₄ ⇒ V₅= π r²* 2r= 2π r² *r= ? , zatem S₅= ³⁴¹₆₄ ⇔ a₁^1−q5_1−q=³⁴¹₆₄ ⇔ 4r²* ⁴₃(1−¹₁₀₂₄)=³⁴¹₆₄ ⇔ r²* ¹⁶₃ *¹⁰²³₁₀₂₄= ³⁴¹₆₄ ⇔ r²= ^3*64*341_64*1023 ⇔ ⇔ r²= 64 i r=8 ⇒ V₅= 2π* 64* 8=1024π cm³− szukana objetość . ...

Agusia: Ale odp jest inna π/2048.

Agusia: Już rozumiem i dziękuję, tam jest błąd powinno być 1/64 czyli r=1/8 Tak mi wyszło. Ale wynik nadal nie wychodzi. Mnie wychodzi V= 2πr²*r=2π*1/64*1/8=π/256