zad Aga: wyznacz wszystkie wartości parametru m, dla których równanie mx²−(m+4)x+¹₄m+¹₄=0 ma dwa różne pierwiastki rzeczywiste, takie ze iloraz ich sumy i iloczynu jest liczbą mniejsza od 2

Aga: Pomóżcie!

Anna: Pomagam.

Anna: Zapisz najpierw układ 3 warunków: 1) a≠0 2) Δ > 0

	x1+x2
3)		< 2
	x1*x2

Spróbuj, a ja też zaraz Ci rozwiążę układ.

Aga: Wychodzą mi dziwne rzeczy czekam na twoje rozwiązanie

Anna: 1) a=m ⇒ m≠0 2) Δ>0 ⇔ b²−4ac > 0

	1		1
[−(m+4)]2 − 4m(		m+		) > 0
	4		4

	2
m2+8m+16−m2−m > 0 ⇒ 7m+16 > 0 ⇒ m> −2
	7

	−b   a
3)		< 2
	c   a

	m+4		m
		*		< 2
	m		1   1   m+ 4   4

	m+4
		− 2 <0
	1   1   m+ 4   4

	1   1   m+4−2( m+ )   4   4
		< 0
	1   1   m+ 4   4

	1   1   m+4− m−   2   2
		< 0
	1   1   m+ 4   4

	1		1		1		1
(		m+3		)(		m+		) < 0
	2		2		4		4

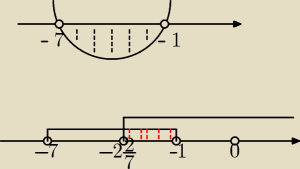
m= −7 m=−1 Na podst. wykresu: m∊ (−7,−1) Po podsumowaniu warunków (część wspólna) − rys. 2 mamy odp.:

	2
m∊ (−2		, −1)
	7