trapez
arek155: 1. w trapezie równoramiennym przekątna ma długość 8 cm i tworzy z dłuższą podstawą kąt o mierze
30o. oblicz pole tego trapezu.
2. w trapezie równoramiennym o długościach podstaw 12 cm i 20 cm przekątne są prostopadłe.
oblicz pole tego trapezu.
27 paź 14:53
ICSP: 1.P = 16
√3
2.P = 256
CO na to powiesz [P{Trivial]]

27 paź 15:03
ICSP: Trivial ?
27 paź 15:03
arek155: ej a możesz mi to rozpisac jak do tego doszłes, z góry dzięki

27 paź 15:04
ICSP: czekamy na potwierdzenie wyników od Triviala
27 paź 15:05
arek155: okej

27 paź 15:05
ICSP: No chyba ze masz odpowiedzi w książce i się zgadzają

27 paź 15:06
arek155: tak zgadza się

więc jak do tego doszłes

?
27 paź 15:09
agata: W pierwszym mi wyszło18√3, a w drugim tak samo.
27 paź 15:13
arek155: a moze mi to ktos rozpisac

27 paź 15:14
agata: W porządku, zgadza się.
27 paź 15:14
arek155: :(
27 paź 15:17
arek155: ICSP możesz mi to rozpisac ?
27 paź 15:18
agata:
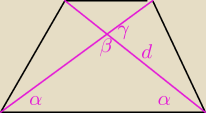
α=30
0 d=8
β=180
0−2α=120
0
γ+β=180
0
γ=60
0
27 paź 15:19
agata:

α=30
0 d=8
β=180
0−2α=120
0
γ+β=180
0
γ=60
0
27 paź 15:20
ICSP:
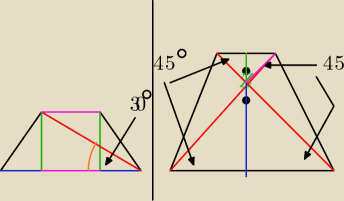
rysunki to podstawa.
Zad1
Rysunek po stronie lewej:
Najpierw wyliczamy z funkcji trygonometrycznych lub z własności trójkąta(to w gimnazjum)
długość odcinka zielonego oraz długość odcinka (różowego+niebieski)
zielony = 4
różowy + niebieski = 4
√3
wprowadźmy oznaczenia:
a = dłuższa podstawa
b = krótsza podstawa
h = wysokosc:
| a+b | |
| *h = P = (różowy + niebieski)*zielony = 4 * 4√3 = 16√3 |
| 2 | |
Tylko nie rysuj tak kolorami w zeszycie bo nauczyciel zawału dostanie.
Zad2
własności trójkąta o kątach 90,45,45 lub też z funkcji trygonometrycznych liczymy długość
odcinków zielonego oraz niebieskiego.
Zaprezentuje zielony
Podstawa na górze ma 12 i jest ona przeciwprostokątną trójkąta prostokątnego którego bok ma
więc 6
√2(odcinek różowy) . Teraz zauważamy ze odcinek różowy jest przeciwprostokątną
drugiego trójkąta o boku(odcinek zielony) = 6
czyli zielony = 6
niebieski = 10
27 paź 15:23
arek155: dzięki wielkie

27 paź 15:24
arek155: ej a jak bedzie z tym ?
1. krótsza podstawa trapezu prostokątnego ma długość 8 cm i jest to 40% długości dłuższej
podstawy. Krótsza przekątna trapezu ma długość 10cm. Oblicz obwód i pole tego trapezu.
2. Pole trapezu równoramiennego jest równe9√3 cm2. Ramię trapezu o długości 2√3 cm tworzy z
dłuższą podstawą kąt o mierze 30o. Oblicz długość krótszej podstawy tego trapezu.
3. Pole trapezu równoramiennego jest równe 39√3cm2. Ramię trapezu o długości 6 cm tworzy z
dłuższą podstawą kąt o mierze 60o. Oblicz długość krótszej podstawy tego trapezu.
27 paź 15:27
agata:
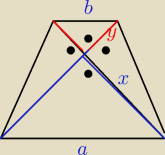
zad.2
a=20
Z Pitagorasa
x
2+x
2=400
x
2=200
x=10
√2
Podobnie b=12
2y
2=144
y−6
√2
| | 1 | | 1 | |
P= |
| x2+U{1}{2{}y2+2* |
| *x*y |
| | 2 | | 2 | |
27 paź 15:29
ICSP: Tak samo

Zrób rysunek a sam zobaczysz.
27 paź 15:30
arek155:
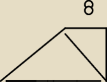
przekątna ma 10 cm a ta dłuzsza podstawa 11,2
nie czaje tej całej matmy

27 paź 15:39
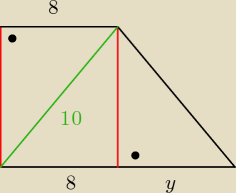
ICSP: Policz długość odcinka czerwonego.
Później policz długość dłuższej podstawy oraz długość odcinka y. Policz długość ramienia i
podaj odpowiedź. Powiem że dłuższa podstawa wcale nie ma 11,2
27 paź 15:45
ICSP:
27 paź 15:47
arek155: czerwony odcinek ma 6
a podstawa 8y ..
27 paź 15:55
agata: Podstawa 8+y, czerwony, czyli wysokość h=6.
27 paź 16:09
ICSP: teraz policz długość dłuższej podstawy.
27 paź 16:12




 więc jak do tego doszłes
więc jak do tego doszłes ?
?

 α=300 d=8
β=1800−2α=1200
γ+β=1800
γ=600
α=300 d=8
β=1800−2α=1200
γ+β=1800
γ=600
 α=300 d=8
β=1800−2α=1200
γ+β=1800
γ=600
α=300 d=8
β=1800−2α=1200
γ+β=1800
γ=600
 rysunki to podstawa.
Zad1
Rysunek po stronie lewej:
Najpierw wyliczamy z funkcji trygonometrycznych lub z własności trójkąta(to w gimnazjum)
długość odcinka zielonego oraz długość odcinka (różowego+niebieski)
zielony = 4
różowy + niebieski = 4√3
wprowadźmy oznaczenia:
a = dłuższa podstawa
b = krótsza podstawa
h = wysokosc:
rysunki to podstawa.
Zad1
Rysunek po stronie lewej:
Najpierw wyliczamy z funkcji trygonometrycznych lub z własności trójkąta(to w gimnazjum)
długość odcinka zielonego oraz długość odcinka (różowego+niebieski)
zielony = 4
różowy + niebieski = 4√3
wprowadźmy oznaczenia:
a = dłuższa podstawa
b = krótsza podstawa
h = wysokosc:

 zad.2
a=20
Z Pitagorasa
x2+x2=400
x2=200
x=10√2
Podobnie b=12
2y2=144
y−6√2
zad.2
a=20
Z Pitagorasa
x2+x2=400
x2=200
x=10√2
Podobnie b=12
2y2=144
y−6√2
 Zrób rysunek a sam zobaczysz.
Zrób rysunek a sam zobaczysz.
 przekątna ma 10 cm a ta dłuzsza podstawa 11,2
nie czaje tej całej matmy
przekątna ma 10 cm a ta dłuzsza podstawa 11,2
nie czaje tej całej matmy
