ostrosłup trójkątny piotrek: Podstawą ostrosłupa jest trójkąt prostokątny o przyprostokątnych 16cm i 12cm. Oblicz objętość tego ostrosłupa, wiedząc, że każda krawędź boczna tworzy z płaszczyzną podstawy kąt 60°. V=1/3*Pp*H Pp = (16*12)/2 = 96 nie wiem tylko jak wyznaczyć tę cholerną wysokość. zrobilbym tak: opisuję okrąg na podstawie. spodek wysokości leży na środku okręgu, z kolei srodek okręgu lezy w polowie przeciwprostokątnej naszego trójkąta. tg60stopni = H/10 => H = 10*√3 pozdrawiam, będę wdzieczny za wszelką pomoc,nie jestem pewien czy moj tok rozumowania jest dobry

Eta: ok

piotrek: http://zadane.pl/zadanie/743588 −> na tej stronie znalazlem to zadanie i twysokosc ma inna wartosc mnie tez się wydaje, ze powinna byc ciut wieksza

sushi_ gg6397228: najlepiej jest narysowac trojkat prostokatny o podanych wymiarach na wierzcholkach polozyc plasteline potem wziąć do reki ołowki/kredki i odmierzyc 60^o i zobaczyc gdzie bedzie wierzcholek bryły

piotrek: wszystko fajnie, ale wystarczy lekka niedokladnosc i łatwo o pomyłkę moglby ktos po swojemu policzyć wysokość? chcialbym miec 100% pewność

sushi_ gg6397228: jak zrobisz to co podalem, to bedziesz wiedziec, ze wysokosc bryły nie lezy na zadnym boku trojkata

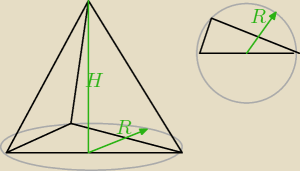
dero2005: Jeśli wszystkie krawędzie tworzą z podstawą jednakowy kąt to spodek wysokości leży na środku przeciwprostokątnej

piotrek: czyli jednak dobrze mowilem?

piotrek: bo z tego co mowisz dero wynika, ze mialem rację, jednak kiedy patrzę na Twoj rysunek, to wydaje mi się, ze sushi dobrze mowi, i ze wysokosc bryly nie lezy wcale na boku trojkata

olek: każda krawędź boczna tworzy z płaszczyzną podstawy kąt 60°, więc wysokość nie może leżeć na przeciwprostokątnej , wtedy 2 kąty miały by 90^o

dero2005: nie wierz w cuda. Myśl samodzielnie. Jeżeli trójkąt prostokątny wpiszemy w okrąg to przeciwprostokątna jest średnicą. Jeżeli wszystkie krawędzie są pochylone pod jednakowym kątem

	H
to tangens tego kąta jest jednakowy dla wszystkich krawędzi tzn tg α =		. Licznik(H)
	R

jest stały więc mianownik (R) też jest taki sam dla wszystkich kątów. Ten rysunek po lewej stronie jest tylko poglądowy. W rzeczywistości jedna ze ścian bocznych(ta oparta na przeciwprostokątnej) jest pionowa tzn tworzy kąt prosty z podstawą.

dero2005: Jeżeli nie możesz sobie tego wyobrazić to narysuj sobie rozwinięcie i sklej model.

jan: z definicji ostrosłupa prostego wynika, że spodek wysokości leży na środku okręgu opisanego na podstawie, a trójkąt prostokątny a środek przeciwprostokątnej w środku okręgu. Olek , coś Ci się pomyliło,sprawdź na modelu

dero2005: najpierw naucz się definicji ostrosłupa prostego i nie mąć ludziom w głowie Ostrosłup prosty to taki, że a) na podstawie można opisać okrąg b) spodek wysokości leży w środku okręgu opisanego

jan: Dero2005, napisz co źle napisałem (oprócz literówek). Czy w tym wypadku "w" i "na" to taka wielka różnica

piotrek: dero, o co Ci chodzi? wydaje mi się, ze jan dobrze wszystko napisał