logika, prawa rachunku zdań xyz: Sprawdź, czy podane zdania są tautologiami: a)(p⇒q)⇔(∼p∧(∼q)) b)(p∧(∼q))⇔(∼(p⇒q)) c)[∼(p∨q)]⇔[(∼p)∨(∼q)] Bardzo proszę o pomoc, nic z tego nie rozumiem.

agata: a) p q p⇒q ∼p ∼q (∼p⋀∼q) (p⇒q)⇔(.....) 1 1 1 0 0 o 0 Dalej nie ma co sprawdzać bo na końcu musi wyjść jedynka przy tautologii. Odp. To zdanie nie jest tautologią

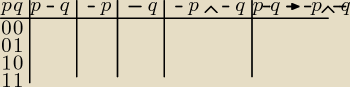
konrad: Rysujesz sobie taką tabelkę. W kolejnych kolumnach wpisujesz poszczególne części tego zdania i sprawdzasz dla nich wartość logiczną. W ostatniej kolumnie masz całe to zdanie (na rysunku trochę nie wyszło) i jeżeli wyjdzie Ci w którymś momencie 0 w tej kolumnie to znaczy, że zdanie nie jest tautologia.

rupert: Tylko w b masz tautologie.

xyz: Czy przy każdym przykładzie trzeba rysować taką tabelkę?

konrad: No raczej.

xyz: Jeszcze jedno pytanie: zdanie jest tautologią wtedy, gdy w czterech wersach w ostatniej kolumnie jest 1?

konrad: Zdanie jest tautologią jeżeli w całej ostatniej kolumnie, czyli tej w której znajduje się wartości badanego zdania, będą same jedynki. Nie musisz robić całej tabelki. Rozwiązujesz wierszami. I jak Ci w ostatniej kolumnie wyjdzie 0 to już nie musisz dalej rozwiązywać bo zdanie nie jest tautologią.

xyz: ok, dziękuję bardzo za pomoc