wartość bezwzględna vladimirovna: |x²−9|+|x²−16|=m Dla jakich wartosci parametru m równanie ma dokladnie 2 rożne pierwiastki http://www.wolframalpha.com/input/?i=|x^2-9|%2B|x^2-16|

vladimirovna: powinno byc (25, +oo) i nie wiem jakim cudem

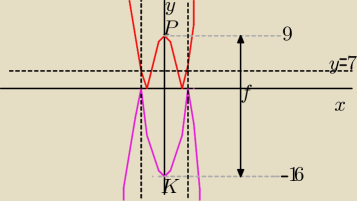
shaka: |x²−9|+|x²−16|=m ⇒ |x²−9|=m−|x²−16| Niech |x²−16|=g(x) i |x²−9|=f(x) Narysuję w jednym układzie współrzędnych wykresy funkcji −g(x) i f(x) zbadam,dla jakich m∊R równanie f(x)=m−g(x) ma 2 różne rozwiązania. Parametr m dobieram w ten sposób,że przesuwam wzdłuż osi 0y jeden z wykresów −g(x) lub f(x)bo m∊y.To nie ma znaczenia,który z nich przesunę,bo równie dobrze mogłem zbadać równanie g(x)=m−f(x). Różnica m∊y jest zawsze ta sama. Ponieważ zapisałem f(x)=m−g(x),więc dobierając m przesuwam wykres −g(x),(fioletowy). Z rysunku odczytuję,że jeśli przesunę −g(x) w górę o mniej ni różnica (16+9=25) tj. m∊(−∞,25),to równanie f(x)=m−g(x) ma 0 lub 4 rozwiązania, dla m=25 ma dokładnie 3 rozwiązania (punkt K pokryje się z P) i wreszcie dla m∊(25;+∞) f(x)=m−g(x) ma dokładnie 2 rozwiązania

shaka: * Uwaga do zad.: Wydaje się,że dla m=7 równanie ma 2 pierwiastki,co nie jest prawdą. |x²−9|+|x²−16|=m ma również 4 rozwiązania:−4,−3,3,4 .Nie widać tego bezpośrednio z rys.Zależy to od tego, jak narysujemy wykres pomocniczy,ja narysowałem akurat f(x)=m−g(x). By jednak zbadać liczbę rozw. równania z sumą wartości bezwzględnych f(x)+g(x)=m ma 2 pierwiastki ∊ R,musimy rozważyć 2 przypadki: f(x)=m−g(x) i g(x)=m−f(x).

vladimirovna: Dzięki wielkie! Bardzo oryginalny pomysł.