Trudne ostrosłupy Zosia: W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem α. Odległość środka podstawy od krawędzi bocznej jest równa d. Oblicz objętość tego ostrosłupa.

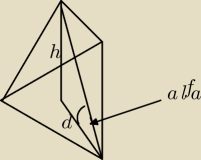
konrad: V=1/3Pph

	a2√3
Pp=
	4

a,h=?

	2
d=		h
	3

	a√3
h=
	2

	2		a√3
d=		*
	3		2

	a√3
d=
	3

3d=a√3

	3d
a=
	√3

	3d√3
a=
	3

a=d√3

	(d√3)2√3
Pp=
	4

	3d2√3
Pp=
	4

tg α=h/d h=tg α*d

	1		3d2√3
V=		*		*tg α*d
	3		4

	3d3√3*tg α
V=
	4

konrad:

	2		a√3
To h w d=		h i h=		, to powinno być hp bo to jest wysokość podstawy.
	3		2

Bogdan: Zadanie przez konrada jest źle rozwiązane. Niewłaściwie jest oznaczona odległość d, ponadto niepotrzebnie wprowadzona jest wysokość h.

	1
R =		a√3
	3

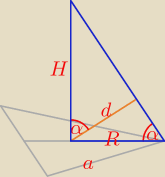
d		d		1		d
	= sinα ⇒ R =		⇒		a√3 =		/*√3
R		sinα		3		sinα

	d√3
a =
	sinα

d		d
	= cosα ⇒ H =
H		cosα

	1		1		1		1		3d2		d
Objętość V =		*		a2√3*H =		*		*		√3*
	3		4		3		4		sin2α		cosα

Zosia: Dziękuję bardzo sama tego bym nie zrobiła.