Równanie z wartością bezwzględną i parametrem Basia: Ile rozwiązań ma równanie w zależność od parametru p: x|x|=x+p

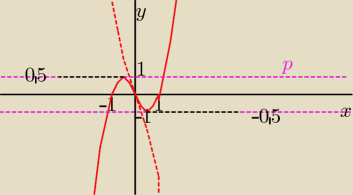
shaka: x|x|=x+p ⇒ x|x|−x=p ⇒ x(|x|−1)=p. Niech x(|x|−1)=f(x). Ponieważ mamy |x| należy rozważyć dwa przypadki; Dla x≥0 x(|x|−1)=x(x−1),natomiast gdy x<0,to x(|x|−1)= x(−x−1)= −x(x+1) Stąd: x(|x|−1)=p ⇔ x(x−1)=p ⋁ −x(x+1)=p Liczbę rozwiązań równania x(|x|−1)=p w zależności od parametru p najwygodniej odczytać z wykresu f(x)=x(|x|−1). Z wykresu odczytujemy,że f(x)=p ma: 1 rozwiązanie ⇔p∊ (−nieskończoności;−0,5)∪(0,5;+nieskończoności) 2rozwiązania ⇔ p=−0,5 ∪ p=0,5 3 rozwiązania ⇔ p∊(−0,5;0.5)

shaka: Poprawka : 1 rozwiązanie ⇔p∊ (−nieskończoności;−0,25)∪(0,25;+nieskończoności) 2rozwiązania ⇔ p=−0,25 ∪ p=0,25 3 rozwiązania ⇔ p∊(−0,25;0.25) Na wykresie pozmieniaj −0,5 i 0,5 na −0,25 i 0,25