algebra
Róża: niech A= 2n−m + (nm +2+mn)*mm2−n2 gdzie m i n są różnymi liczbami
naturalnymi. Uzasadnij, że odwrotność liczby A jest liczbą naturalną
23 paź 21:09
Eta:
| | 2 | | n2+2mn+m2 | | m | |
A= |
| + |
| * |
| = |
| | n−m | | mn | | (m−n)(m+n) | |
| | 2 | | (m+n)2 | | m | | m+n | | 2 | |
= |
| + |
| * |
| = |
| − |
| = |
| | n−m | | mn | | (m−n)(m+n) | | n(m−n) | | m−n | |
| | m+n−2n | | m−n | |
= |
| = |
| = .......... |
| | n(m−n) | | n(m−n) | |
23 paź 22:37
Róża: nie rozumiem tego przekształcenia w drugiej linijce.... możesz wytłumaczyć?
23 paź 22:57
Eta:
(n−m) = −(m−n) .... o to Ci chodziło?
23 paź 22:58
Eta:
wcześniej upraszczasz ułamki przy mnożeniu

23 paź 23:00
Róża: nie, o to: 2n−m +(m+n)2mn* m(m−n)(m+n)=m+nn(m−n)−2m−n
23 paź 23:10
Eta:
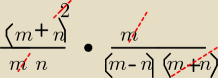
23 paź 23:16
23 paź 23:17
Róża: aha

dzieki Eta zawsze można na Ciebie liczyć

23 paź 23:20
Eta:

23 paź 23:21
Róża: jak masz jeszcze siły to mi podpowiedz z tym coś: uzasadnij, że jeśli liczby a, b i c różne od
zera tworzą w podanej kolejności ciąg geometryczny, to:
| | 1 | | 1 | | 1 | |
a2b2cc( |
| + |
| + |
| ) = a3+b3+c3 |
| | a3 | | b3 | | c3 | |
23 paź 23:29
Eta:
a,b,c −−− tworzą ciąg geom, => b
2=a*c
| | b3c3+a3c3+a3b3 | | b3c3+a3c3+a3b3 | |
= |
| = |
| = |
| | abc | | b3 | |
| | (ac)3 | | (b2)3 | | b6 | |
= c3+a3+ |
| = a3+c3+ |
| =a3+c3+ |
| = |
| | b3 | | b3 | | b3 | |
= a
3+b
3+c
3
24 paź 00:03
Eta:
Podam prościej:
b
2=a*c to: a
2*b
2*c
2= a
2*ac*c
2= a
3*c
3
| | 1 | | 1 | | 1 | | a3c3 | |
a3*c3( |
| + |
| + |
| )= c3+ |
| +a3= |
| | a3 | | b3 | | c3 | | b3 | |
| | (ac)3 | | (b2)3 | | b6 | |
= a3+c3+ |
| = a3+c3+ |
| = a3+c3+ |
| = |
| | b3 | | b3 | | b3 | |
= a
3+b
3+c
3
c.n.u
24 paź 01:07

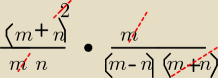
 dzieki Eta zawsze można na Ciebie liczyć
dzieki Eta zawsze można na Ciebie liczyć
