Oblicz. ania: Punkty A,B,C takie,że A=(5,8) ,B=(−1,2) ,C=(2,−1),są kolejnymi wierzchołkami prostokąta ABCD. a)Wyznacz współrzędne środka symetrii prostokąta ABCD. b)Wyznacz współrzędne wierzchołka D. c)Oblicz promień R i pole P koła opisanego na tym prostokącie. d)Wyznacz sinα,który tworzy przekątna AC z bokiem CD. ZADANIE MATURALNE.

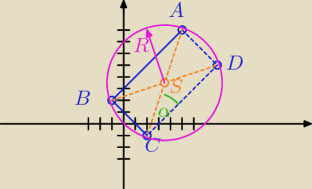
dero2005: a) środek symetrii prostokąta (punkt S) obliczamy jako środek odcinka |AC| wg wzoru

	xA+xC		yA+yC		5+2		8−1
S = (		,		) = (		,		)
	2		2		2		2

S = (3,5 , 3,5) b) współrzędne wierzchołka D − liczymy wspórzędne wektora BC→ BC→[a,b] = [x_C−x_B , y_C−y_b] = [2+1 , −1−2] = [3 , −3] w prostokącie przeciwległe boki są równe i równoległe, więc współrzędne wektorów BC→ i AD→ są równe i możemy je porównać AD→[x_D−x_A, y_D−y_A] = [a,b] = [3 , −3] x_D−5 = 3 x_D = 3+5 = 8 y_D−8 = −3 y_D = −3+8 = 5 D = (8 , 5) c) promień R jest równy długości odcinka np.|SA| długość odcinka |SA| liczymy ze wzoru d = R = √(x_S−x_A)² + (y_S−y_A)² = √(3,5−5)² + (3,5−8)² = = √(−1,5)² + (−4,5)² = √2,25 + 20,25 = √22,5 P = πR² = π*22,5² = 506,25π d) sinus kąta α

	|AD|
sin α =
	|AC|

|AD| = √(x_D−x_A)² + (y_D−y_A)² = do policzenia |AC| = √(x_C−x_A)² + (y_C−y_A)² = do policzenia

ania: Dziękuję za zrobienie tego zadania.Jestem pełna podziwu .

dero2005: bez jaj

dero2005: jakby to było zadanie maturalne to wszyscy by zdali maturę