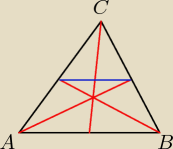
planimetria Joe: Ciekawi mnie coś takiego jak na rysunku, mianowicie czy da się obliczyć jakoś środkowy odcinek w trójkącie równobocznym? Jak na rysunku teoretycznie według mnie środkowy odcinek to ten niebieski. Wie ktośmoże jak go obliczyć? Przy długości boku trójkąta równobocznego 6?

am: czy chodzi ci o odcinek laczacy srodki ramion trojkata rownobocznego (lub innego) ?

am: jesli tak to jego dlugosc to polowa dlugosci podstawy do ktorej jest równolegly

am: czyli 3

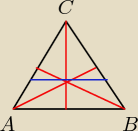
Joe: Ajć sorki, chodziło mi o odcinek przechodzący przez środek ciężkości trójkąta, teraz chyba poprawnie

am: to można z podobienstwa wyznaczyć

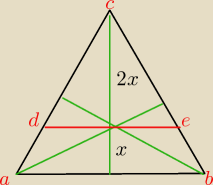
am: trojkat dec jest podobny abc w skali 2/3 zatem DE=2/3|AB|

Joe: mógłbyś pomóc bo nie mam pojęcia

	a√3
h =
	2

1^o a = 6 h = 3√3 2^o

	2		2
hx =		* h =		* 3√3 = 2√3
	3		3

x = ?

	2√3		6
k =		=
	3√3		x

Tak jakoś?

am: masz wyzej

Joe: Z twojego za bardzo nie wiem o co chodzi (na jakiej podstawie) ale u mnie można zrobić:

2√3		3√3
	=
x		3

9x = 18 / : 9 x = 2 (to jedna połówka,więc całość to 4 jak u Ciebie )

am: Środkowe trójkąta przecinają się w jednym punkcie. Dzieli on każdą z nich w stosunku 2:1 licząc od wierzchołka. Znasz to twierdzenie ? Ja z niego skorzystalem i podobienstwa krotko

Bogdan:

	1
R =		a√3
	3

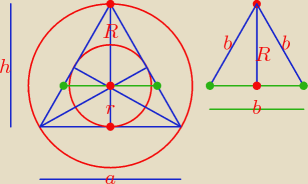
W trójkącie równobocznym środek ciężkości, ortocentrum, środek okręgu opisanego i środek okręgu wpisanego pokrywają się. Jeśli bok trójkąta równobocznego ma długość a, a szukana długość jest równa b, to b jest bokiem trójkąta równobocznego, którego wysokość jest równa R.

	1		1		1		2
R =		b√3 ⇒		b√3 =		a√3 /*		⇒ b = ...
	2		2		3		√3

albo prościej:

	2
skala podobieństwa trójkątów równobocznych o bokach długości b i a jest równa
	3

	2
(bo R =		h),
	3

	b		2
to		=		⇒ b = ....
	a		3