Joe
Joe: Mam takie zadanie:
"Ze zbioru {1,2,3,4,5,6,7} losujemy trzy razy po jednej liczbie bez zwracania. Oblicz
prawdopodobieństwo zdarzenia, że suma wylosowanych liczb będzie liczbą parzystą."
Rozwiązanie jest następujące:
| | | |
i mam pytanie: skąd wzięło się: 1 + | * 3 szczególnie nie wiem skąd ta jedynka i dlaczego |
| | |
tu jest mnożenie. Bardzo proszę o pomoc.
22 paź 13:58
Joe: Błagam o pomoc
22 paź 14:13
sushi_ gg6397228:
najlepiej rozpisac sobie przypadki i nie patrzec na rozwiazania, bo moze byc nie do tego
zadania
22 paź 14:14
sushi_ gg6397228:
tam powinno byc jeszcze cos do tej 1
22 paź 14:17
22 paź 14:18
sushi_ gg6397228:
to poczytaj co napisali −−> podzial na
parzyste (ile jest mozliwosci)
+ 2nieparzyste(ile ich jest) * parzysta (ile ich jest)
22 paź 14:21
Joe: Ok już prawie rozumiem, tylko jeszcze jedno pytanie: dlaczego mnożymy parzysta przez te dwie
nieparzyste?
22 paź 14:25
sushi_ gg6397228:
to sobie wypisz na piechote wszystkie mozliwosci a potem zobacz
a jak mamy chłopcy i dziewczynki wybor to tez mnozysz:
22 paź 14:27
Joe: I mam jeszcze tako jedno zadanie:
"Punkty C = (6,6) i D = (2,4) są krańcami krótszej podstawy trapezu równoramiennego ABCD.
| | 1 | |
Dłuższa podstawa należy do prostej opisanej równaniem y = |
| x − 2. Ramię trapezu ma |
| | 2 | |
długośćrówną
√40. Wyznacz współrzędne wierzchołków A i B."
No to zrobiłem to zadanie, mianowicie:
odległość punktów A i D to
√40 zatem:
| | 1 | |
√40 = √(x−2)2 + ( |
| x−6)2 |
| | 2 | |
i wyszły mi dwa wyniki
| | 32 | |
A(0,−2) i drugi A( |
| , ...) |
| | 5 | |
Tam samo obliczyłem punkt B.
I tutaj moje pytanie dlaczego w odpowiedziach podane są te ładne wyniki − tj.: A(0,−2) a nie ma
tych z ułamkami. W szkole mnie uczono,że trzeba dwa wypisywac zawsze.
22 paź 14:30
Joe: Teraz już rozumiem to zadanie z prawdopodobieństwa
dziękuje, mógłbyś jeszcze
pomóc z tym drugim?
22 paź 14:35
sushi_ gg6397228:
| | 1 | | 1 | |
punkty to (x, |
| x − 2) a nie (x, |
| x ) |
| | 2 | | 2 | |
22 paź 14:44
sushi_ gg6397228:
do obliczenia AD, ma sie rozumiec
22 paź 14:45
sushi_ gg6397228:
bo zobacz na rysunek, gdzie te punkty powstaja−−> czy dostaniesz wtedy trapez
22 paź 14:46
sushi_ gg6397228:
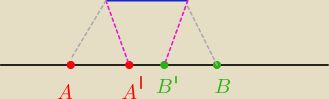
wiec widac ze A' i B' nie moga byc bo |A'B'| bedzie krotszy niz |CD|
22 paź 14:50
agata: Punkt A, który leży nadanej prostej ma współrzędne (x,U{1}[2}x)
podobnie D. Metoda jest dobra.Może trzeba sprawdzić, czy oba punkty należą do danej prostej.
22 paź 14:55
agata: | | 1 | |
A(x, |
| x−2) i dalej sprawdzić,czy spełniony jest drugi warunek. |
| | 2 | |
22 paź 14:57
Joe: Ok bardzo wam dziękuje
A wiesz może sushi jak obliczyć AnB gdzie mam tylko podane, że
P(A) = 155 oraz P(B) = 403
22 paź 15:18
sushi_ gg6397228:
i jeszcze powinna byc podana moc omega; wtedy
P(AuB)= P(A)+P(B)− P(AnB)
22 paź 15:21
Joe: jest podana:
|Ω| = 2013
tylko nie miałem jeszcze tego typu zadań, mógłbyś pokazać jak to nalezy zrobić?
22 paź 15:29
Joe: Pomocy
22 paź 15:42
sushi_ gg6397228:
to ile jest elementow poza zbiorem
bo jeszcze czegos brakuje bo P(AnB) moze byc maksymalnie 155
22 paź 15:45
Joe:
Mam tylko to podane:
P(A) = 155
P(B) = 403
|Ω| = 2013
i mam za zadanie obliczyć AnB
22 paź 15:47
sushi_ gg6397228:
a jakie sa odpowiedzi A, B, C, D,
22 paź 16:06
