Oblicz promień R,i pole P? nina: Na trójkącie ABC opisano okrąg.Wyznacz współrzędne środka tego okręgu ,oblicz promień R i pole P koła ograniczonego tym okręgiem ,gdy A=(−3,2).B=(−5,0),C=(1,−2).

Tadeusz: S(x_s, y_s) (−3−x_s)²+(2−y_s)²=R (−5−x_s)²+(0−y_s)²=R (1−x_s)²+(−2−y_s)²=R .... i walcz

nina: A czy mogłabym prosić o dalsze wytłumaczenie ,jestem słaba jeżeli chodzi o matematykę .

nina: proszę o pomoc.

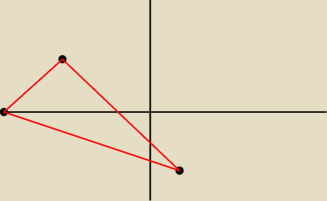
Tadeusz: ... ale można i inaczej Jak policzysz długości boków to okaże się, że trójkąt jest prostokątny... a jeżeli tak to AC jest średnicą okręgu opisanego ...

nina: Dalej pustka w głowie .Z czego mam policzyć długości boków.

Tadeusz: https://matematykaszkolna.pl/strona/1248.html

nina: Dziękuję za podpowiedz ,skończę to zadanie jutro,dam odpowiedż ,jakby coś było żle to mogę liczyć na dalsze wskazówki?

agata: Tadeusz, w tych wzorach powinno być R².

Gustlik: Jest drugi sposób wyznaczenia współrzędnych środka okręgu opisanego na trójkącie. Okrąg opisany ma środek w punkcie przecięcia się symetralnych boków. Wyznaczamy równania symetralnych dwóch dowolnych boków tego trójkąta, a potem z tych równań układamy układ. Rozwiązaniem tego układu są współrzędne srodka. A=(−3,2) B=(−5,0) C=(1,−2) Wyznaczam symetralną boku AB:

	yB−yA		0−2		−2
aAB=		=		=		=1
	xB−xA		−5+3		−2

	yA+yB
Środek AB S1=(U(xA+xB}{2},		)=(−4, 1)
	2

wsp. kierunkowy symetralnej:

	1
a2=−		=−1 (z war. prostopadłości prostych)
	aAB

Równ. symetralnej AB: y=−x+b podstawiam współrz. środka S₁ 1=4+b b=−3 y=−x−3 Liczę symetralną innego boku, np. AC w ten sam sposób:

	−2−2		−4
aAC=		=		=1
	1+3		4

środek AC S₂=(−1, 0)

	1
a2=−		=1
	aAC

Równ. symetralnej y=x+b 0=−1+b b=1 y=x+1 { y=−x−3 { y=x+1 −x−3=x+1 −2x=4 x=−2 y=2+1 y=3 Środek okręgu S=(−2, 3) Promień np. r=|SA^→| A=(−3,2) S=(−2, 3) Liczę współrzędne wektora SA^→ SA^→=[−3+2, 2−3]=[−1, −1] r=√(−1)²+(−1)²=√2 Pole = πr²=2π