f(A) i f(B) Martyna: Oznaczmy przez f(A) zbiór wszystkich liczb, które są wartościami funkcji f dla argumentów ze zbioru A, tzn. f(A)={f(x):x należy do A}. Niech f(x)=1/2 *x³−x²−2x+4. Niech A=<1;3>, B=<−2;1> a) Znajdź f(A) i f(B) b) Sprawdź, czy f(A\B)=f(A)\f(B)

think:

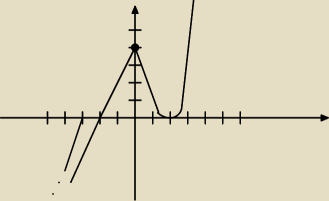
	1		1		1
f(x) =		x3 − x2 − 2x + 4 =		x2(x − 2) − 2(x − 2) =		(x2 − 4)(x − 2) =
	2		2		2

	1
		(x − 2)2(x + 2)
	2

	1
f(A) = <0, 2		>
	2

f(B) = <0,4>

	1
f(A\B) = <0, 2		>
	2

f(A) \ f(B) = zbiór pusty