Patt:
Nie radzę sobie z mechaniką − w zasadzie to fizyka. Proszę o pomoc.
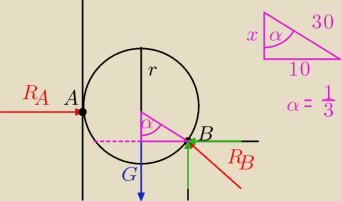
Gładka kula o r=30cm i ciężarze G=24N opiera się o pionową ścianę w punkcie A i poziomą krawędź
w punkcie B, Wyznacz reakcje w punktach podparcia kuli jeżeli punkty podparcia są oddalone od
siebie o a=40cm.
Zrobiłem rysunek do tego.
Dane do rysunku:
R
A − reakcja A działająca na punkt A
R
B − reakcja B działająca na punkt B
G− ciężar kuli =24N
r− promień kuli
Zielone strzałki − składowe reakcji R
B
Wiem tylko tyle, że zadanie ma być obliczone w taki sposób:
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Od tego momentu nie wiem co się w zadaniu dzieje
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
∑Fix=0
∑Fiy=0
R
A−R
B*sinα=0
R
B*cosα−G=0
R
A=R
B*sinα=G*tgα
Zadanie rozwiązane, ale nie rozumiem jak do tego doszło. Proszę o pomoc w tłumaczeniu tego
zadanka. Zajrzę wieczorem i postaram się zrozumieć.
Z góry dziękuję każdemu kto chociaż spróbuje.
rupert: Aby liczyć tego typu zadania należy na samym początku uwolnić każde ciało nieswobodne od
więzów, a więzy zastąpić reakcjami, uwzględniając przy tym jaka to jest reakcja: czy normalna,
czy występuje tarcie, czy powierzchnia jest gładka czy chropowata, jeśli są przeguby to jakie:
przesuwne czy stałe, jeśli są to pręty czy liny i ciało jest uwiązane należy rozpatrzyć czy
występuje ściskanie czy rozciąganie.
Na twoim rysunku masz to uwzględnione: występują reakcje normalne bez tarcia, stąd siły
prostopadłe do powierzchni plus siła ciężkości działająca na ciało.
W następnej kolejności rozpisujesz sumę rzutów sił na oś x oraz oś y, pamiętając przy tym, że
suma musi równać się 0, uwzględniamy również zwroty sił, jeśli siła ma taki sam zwrot jak oś
to mamy + jeśli zwrot jest przeciwny −, jeśli rozkładamy wypadkową R na dwie składowe Rx oraz
Ry to korzystamy z funkcji sin i cos
Wyliczasz niewiadome z równań, podstawiasz dane, wyliczasz i w zasadzie to wszystko.
Przedstawione zadanie jest z zasadzie proste, bo ma raptem dwie niewiadome, bywają takie, że
tych niewiadomych jest więcej niż dwie i to w jednym równaniu, więc trzeba trochę
pokombinować.
