Napisz równanie okregu który jest opisany na trójkącie ABC
WhatS: Napisz równanie okręgu, który jest opisany na trójkącie ABC, gdy A=(4,2) B=(2,4) C=(0,4)
bardzo pilnie potrzebuję tego na jutro, więc jak ktoś da radę to rozwiązać, będę niezmiernie
wdzięczny

19 paź 21:24
Dawid: Obliczyć wystarczy tylko środek okręgu i promien. podstawić do ogólnego wzoru na okrąg i koniec
zadania.
19 paź 21:26
WhatS: no wiem, ale nie ogarniam tego...
a potrzebuję na jutro , bo to na ocene

19 paź 21:27
Dawid: Etapami wygląda to tak:
Znaleźć dwie proste
k przechodzaca przez punkt np A i B
i l; przechodzaca przec A i C
nastepnie znaleźć równania prostych przechodzących przez środki tych boków i prostopadłych do
nich. Nastepnie punkt przeciecia sie tych prostych. Punkt ten bedzie srodkiem okregu.
Długośc od srodka do punktu A lub B lub C to promien
ogólny wzór na okrąg o ile pamietam to (y−A)
2+(x−B)
2=r
2 co do wzoru nie jestem pewien

19 paź 21:32
agata: Jeśli umiesz rozwiązywać równania z trzema niewiadomymi to z układu byłoby chyba szybciej.
19 paź 21:39
krystek: lub (4−a)2+(2−b)2=r2
(2−a)2+(4−b)2=r2
(0−a)2+(4−b)2=r2
Ale nie wiem czy szybciej.
19 paź 21:43
Dawid: Sposobów jest wiele

19 paź 21:44
Eta:
o: x2+y2−2ax−2by+c=0
dla A(4,2) mamy: 42+22−8a−4b+c=0 => 8a+4b −c −20=0
dla B( 2,4) 22+42−4a−8b+c=0 => 4a+8b−c−20=0
dla C(0,4) 02+42−2a*0−2*4b+c=0 => c=8b −16
rozwiązując układ tych trzech równań wyznacz a, b, c
S(a,b) r2= a2+b2−c
o: (x−a)2+(y−b)2=r2
powodzenia w rachunkach
poprawna odp: o: ( x−1)2+(y−1)2= 10
19 paź 21:48
krystek: Oczywiście.
19 paź 21:48
Eta:
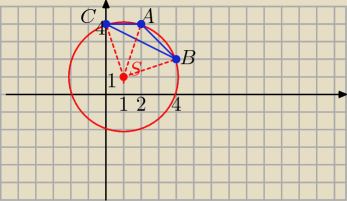
19 paź 21:57
agata: 16−8a+a2+4−4b+b2=4−4a+a2+16−8b+b2
a2+16−8b+b2=4−4a+a2+16−8b+b2
−4a+4b=0
Z drugiego a=1
b=1
r2=1+32
Równanie okręgu (x−1)2+(x−1)2=10
19 paź 22:01
WhatS: Boże, kocham Was, dzięki wielki !

20 paź 07:32





