Oblicz długość krawędzi podstawy w ostrosłupie prawidłowym czworokątnym.
Bartek: Pole powierzchni bocznej prawidłowego ostrosłupa czworokątnego jest równe 96, a wysokość tego
ostrosłupa H=2√5. Wyznacz długość krawędzi podstawy ostrosłupa. Proszę o szybką pomoc.
19 paź 15:30
:-):
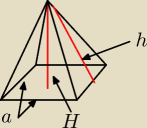
Z Pitagorasa: (1/2a)
2 + H
2 = h
2
Nie wiem czy pole boczne to pole wszystkich bocznych krawędzi czy tylko jednej. Jeżeli tylko
jednej to:
Pole powierzchni bocznej = 1/2 a h = 96
Jeżeli wszystkich to:
P=4*(1/2)ah = 96
Z tych równań już wyznaczysz a.
20 paź 18:56
dero2005:
H = 2
√5 → wysokość
P
b = 2a*h
s = 96 → pole pow bocznej
z tw Pitagorasa
h
s2 = H
2 + (
a2)
2
h
s2 = (2
√5)
2 +
a24
(
48a)
2 = 20 +
a24
| 2304 | | a2 | |
| = 20 + |
| |*4a2
|
| a2 | | 4 | |
9216 = 80a
2 + a
4
t = a
2 >0
t
2 + 80t − 9216 = 0
Δ = 43264
√Δ = 208
t
1 = 64
t
2 = − 144 → odrzucamy
a
2 = 64
a =
√64 = 8
20 paź 21:25