funkcje K.M.L: witam mam pytanie jak rozwiązać to zadanie poniżej Dla jakich wartości parametru a równanie |x−1|=a²−4a−1 ma dwa dodatnie pierwiastki? ale... przy pomocy wykresu f(x)=|x−1| ? Rozwiązałem już inną dłuższą metodą i wyszło dobrze , w odpowiedziach piszą że można to zrobić szybciej rysując wykres, wytłumaczyłby ktoś takie rozwiązanie ,co muszę zrobić po kolei? Pozdrawiam.

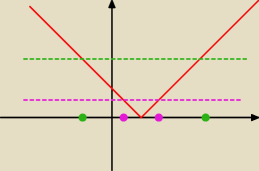
agata: Za a podstawiasz jakąś liczbę i rysujesz wykres funkcji stałej. Na fioletowo zaznaczono dwa rozwiązania dodatnie, a na zielono dodatnie i ujemne. Widać, że 0<a²−4a−1<1.Rozwiąż tę podwójną nierówność i otrzymasz odpowiedź

K.M.L: okej dziękuje .

Solymalhio: Rozwiązanie algebraiczne, nie zgadza się z powyrzszą tezą: 1. x − 1 = a² − 4a − 1 2. x−1 = − (a² − 4a − 1) 1. x = a² − 4a > 0 a₁ = − 2 − {3} < 0 a₂ = − 2 + {3} < 0 1. Nie zgodne z załorzeniami 2. x = −a² + 4a + 2 > 0 a₁ = 2 + {6} >0 a₂ = 2 − {6} > 0 2. Jest zgodne z załorzeniami Odp. x∊ ( 2 − {6}; 2 + {6} )

Artur z miasta Neptuna: Solymalhio −−− jak ty obliczasz miejsca zerowe? a² − 4a = a(a−4)

Solymalhio: Obliczałem to Δ, zawsze mnie zastanawiało jak to możliwe, że obliczając miejsca zerowe na dwa różne sposoby otrzymujemy inne wyniki, choć w rezulatacie nie wiele się różniące od siebie: 1. Miejsca zerowe po obliczeniu Δ : x₁ = 2 − √3 = 0,27 x₂ = 2 + √3 = 3,73 2. Obliczone twoim sposobem: x₁ = 0 x₂ = 4 Magia matematyki =) Ja chciałem zwrócić uwagę na błędne załorzenie w tym zadaniu: agata sugeruje, że aby uzyskać wynik powyższego równania, należy obliczyć nierówność 0<a² − 4a − 1 <1 co jest niespójne z obliczeniami algebraicznymi Ponieważ punktami wykresu w którym rozwiązaniem są dwie liczby dodatnie to: x = 1 y=0 to wg. mnie wystarczyłoby tylko podstawić wartość x, czyli nierówność powinna wyglądać tak: a²−4a−1<1 Czyli x∊ ( 2 − √6; 2 +√6 ) Jeśli się mylę to proszę mi to udowodnić =0

Artur z miasta Neptuna: Solymalhio: Δ = b² − 4ac = 4*2 − 0 = 16 √Δ = 4

	4−4
a1 =		= 0
	2

	4+4
a2 =		= 4
	2

Solymalhio: W porządku masz rację, jednak ja chciałem zwrócić w tym zadaniu uwagę na zupełnie coś innego...

BS: Solymalhio! Wstaw sobie a=0, które spełnia twoje równanie a²−4a−1<1 podczas gdy wyjściowe równanie |x−1|=a²−4a−1 nie będzie spełnione, bo |x−1| ≠ −1, więc się mylisz!

Solymalhio: Jeśli zero nie spełnia równania, to znaczy, że mam rację =) Pozdroo =0 Czytaj ze zrozumieniem =0

Solymalhio: Włąściwie to chyba nikt z was nie zrozumiał, czego chciałem dowieść w powyższym zadaniu =)