zespolone gosia: Oblicz pierwiastki wykorzystując postać trygonometryczną liczby zespolonej. Wyniki podaj w postaci algebraicznej. a) ³√−27i b) ⁴√−4 odp. a) 3i, −3/2(√3+i), 3/2(√3−i) b) 1+i, 1−i, −1−i,−1+i

ICSP: :(( Trzeba z postaci trygonometrycznej?

gosia: tak jest w poleceniu:(

Trivial: :(

ICSP: 0 −27i |z| = 27

	3π
q =
	2

n = 3

	3π		3π
0 − 27i = 27(cos		+ i sin		)
	2		2

no to zaczynamy pierwiastkować, ogólnie wzór jest następujący:

	q + 2kπ		q + 2kπ
n√z = n√|z|(cos		+ isin		)
	n		n

	π		π
z1 = 3√27(cos		+ isin		) = 3(0+i) = 3i
	2		2

	−π		−π		√3		1		3(√3−i)
z2 = 3√27(cos		+ isin		) = 3(		−		i) =
	6		6		2		2		2

	−5π		−5π		−√3		1		−3(√3+i)
z3 = 3(cos		+ isin		) = 3(		−		i) =
	6		6		2		2		2

ICSP: nie lubię postaci trygonometrycznej:(( Jest taka nudna. Drugie analogicznie

gosia: a skąd to: q =3π/2 ?

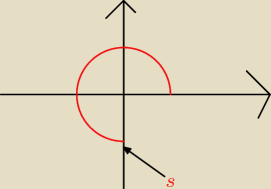
ICSP: strzałka oznacza położenie liczby 0 − 27i to s nic nie oznacza nie wiem w ogóle co tam robi

	3π
kąt czerwony to właśnie		= 270o
	2

przechodzenie z postaci kanonicznej do trygonometrycznej polega właśnie na znalezieniu miary tego kąta

Trivial: LOOL strzałki

ICSP: osi nie oznaczyłem... i co masz do strzałek?

Trivial: Takie fajne. krzywe.

gosia: juz rozumiem, wielkie dzięki za pomoc mam nadzieję, że jakoś sobie poradze jutro na 1 studenckim kolokwium z matematyki

ICSP: Może nie każdy ma talent do rysowania strzałek To nie takie proste, zresztą liczy się przesłanie rysunku a nie jego perfekcyjne wykonanie