trapez równoramienny !! muuuusze: W trapezie równoramiennym długości podstaw są równe 5 i 3cm. Oblicz promień okręgu opisanego na tym trapezie, jeśli kąt ostry ma miarę 30

Dawid: Juz pomagam w miarę możliwości

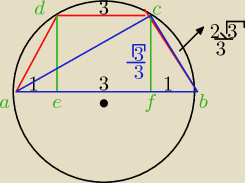
amylaz: Oblicz na rysunku z twierdzenia Pitagorasa boki trójkąta abc i jego Pole. Potem skorzystaj ze wzoru P_Δ=(abc)/4R

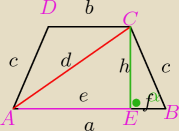
agata: AB=a =5, f=1, e=4

	f
cos300=
	c

	2√3
c=
	3

	1
h=		c
	2

d²=e²+h² Promień okręgu opisanego na tym trapezie jest równy promieniowi okręgu opisanego na trójkącie ABC.

	acd
R=
	4P

	1
Gdzie P=		a*h
	2

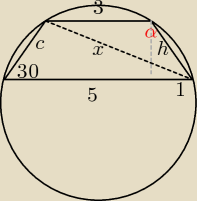
Dawid: Promien okręgu opisanego na trapezie rowniez jest promieniem okregu opsanego na trojkacie powstalym z podstawy trapezu, ramiienia i przekatnej.

	x
a wiec r=
	2sinα

z własnosci ze jest to trapez wpisany w okrag suma przeciwleglych katow rowna jest 180 a wiec α=150

	1		h
mozemy obliczyc z latwoscia h,		=
	sin60		sin30

	1
h=
	√3

z tw pitagorasa wyliczamy x h²+4²=x²

	1
x2=16
	3

	7
x=
	√3

x
	=r sin150=0,5
2sin150

x=r

	7
r=
	√3

agata: Tak można rozwiązać pod warunkiem, że ktoś miał wzory redukcyjne i twierdzenie sinusów.