ciągi Hanka: Dane jest równanie x⁴−10x²+m=0. Wyznacz te wartości parametru m, dla których równanie to ma cztery pierwiastki, z których można utworzyć ciąg arytmetyczny.

Jolanta: za x² podstawiam a a²−10am+m=0 policzΔ i perwiastki

Hanka: nie wychodzi mi coś. wszystko się miesza xD

ICSP: a² − 10a + m = 0 teraz licz te pierwiastki

krystek: Ale jakie warunki ,aby były cztery i tworzyły ciąg geometr.

Hanka: no tak wiem, że Jolanta miała błąd w zapisie. ale wychodzi mi kosmos xD A całą treść zadania podałam.

krystek: A pokaż swoje obl ,poprawie błąd.

Hanka: lepiej pokaż jak ty byś to zrobił

Bogdan: x⁴ − 10x² + m = 0, a = 1, b = −10, c = m Założenia: (1) Δ > 0 ⇒ 100 − 4m > 0 ⇒ m < 25

	c
(2) x1*x2 > 0 ⇒		> 0 ⇒ m > 0
	a

	−b
(3) x1 + x2 > 0 ⇒		> 0 ⇒ 10 > 0 ⇒ m∊R
	a

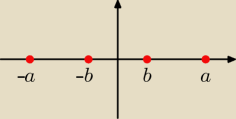
Z (1) i (2) i (3): 0 < m < 25 Cztery miejsca zerowe krzywej: y = ax⁴ + bx² + c układają się symetrycznie względem zera. Ciąg arytmetyczny (a_n): a₁ = −a, a₂ = −b, a₃ = b, a₄ = a. Z własności ciągu arytmetycznego: −2b = −a + b ⇒ a = 3b Postać iloczynowa: (x + a)(x + b)(x − b)(x − a) = 0 ⇒ (x² − a²)(x² − b²) = 0 (x² − 9b²)(x² − b²) = 0 ⇒ x⁴ − 10b²x² + 9b⁴ = 0 −10b² = −10 ⇒ b² = 1 m = 9b² = 9 Odp.: m = 9

Hanka: nie kumam co się skąd bierze