granica funkcji Tomek: Witam mógłby mi ktoś napisać jak udowodnić albo jak rozpisać granice funkcji, w której granica nie istnieje: np w przykładzie:

	x2+x−2		(x+2)(x−1)		(x−1)
lim(x→−2)		=		=
	x3+4x2+4x		x(x2+4x+4)		x(x+2)

no i z tego wynika ze granica nie istnieje ale jak to poprawnie napisać? wystarczy jakoś symbol nieoznaczony napisać czy jakieś granice jednostronne trzeba wyznaczać?

Rivi: Na moje oko to ten ciąg dąży do nieskończoności (jeśli x idzie od −∞)

Tomek: no ale x dąży do −2

Rivi: dąży ale nie osiąga... na górze wtedy masz jakieś tam liczby ujemne, a na dole masz liczbę ujemną*ujemną −> zera nie będzie, bo x nigdy nie będzie −2, co najwyżej 2,0...01 czyli, będzie

	−3,1
tam np		co da dużą liczbę −> i jak będzie się zbliżać x do −2 to
	−2,00005*(−0,00005)

ta liczba będzie coraz większa

Jack: policz granice obustronne przy x→−2⁻ oraz x→−2⁺. Jeśli wyjdą różne nieskonczoności (tzn. z różnym znakiem),to granica nie istnieje ;>

Tomek: ale w odpowiedziach mam że "nie istnieje"

Rivi: No tak, ja przyjąłem, że x pędzi tylko lewostronnie Zwracam honor

Tomek: a w tych granicach obustronnych chodzi o to ze jak wychodzi 0 ale jest x→−2⁻ to granica wynosi −∞ a jak z + to +∞

Tomek: jeszcze jedno pytanko jak mam typ obliczania granic z pierwiastkami to ten wzór działa tylko jak jest (pierwiastek − pierwiastek) czy można go sobie przerobić jak jest (pierwioastek + pierwiastek)?

Jack: dla x→−2⁻ bierzesz liczbę troszkę mniejszą od −2 i sprawdzasz znak całego wyrażenia. Dla x→−2⁺ liczbę troszkę większą i również sprawdzasz znak całości. Mając znak dopisujesz go do symbolu "∞". W ten sposób raz dostaniesz "−∞" a drugim razem "+∞", a zatem wywnioskujesz że skoro granica obustronne są różne, to granica nie istnieje.

Rivi: Jak przerobisz tak, żeby dało się coś skrócić to możesz zawsze. Zaraz Ci rozrysuje granice lewo i prawo stronne... i nie działa to tak jak napisałeś −> jak dąży od −∞ do czegoś to może być zarówno granicą −∞ i +∞

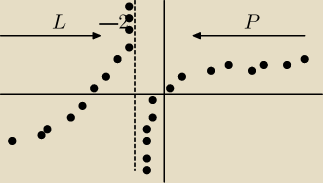
Rivi: L−> granica lewostronna R−> prawostronna tam są hiperbole zamiast kropek