równanie
t.: dla jakich wartości parametru m pierwiastki równania x2−4(m+1)x+2m(m−1)=0 spełniają warunek
x1<m<x2?
16 paź 14:10
t.: pomóżcie.
policzyłam, że:
Δ=m2+5m+2
ale nie mogę obliczyć x1 i x2, bo wychodzi mi brak pierwiastków.
16 paź 14:48
Godzio:
Δ > 0
f(m) < 0
Część wspólna i masz wynik
16 paź 15:08
t.: a dlaczego f(m)<0?
16 paź 15:17
Godzio:
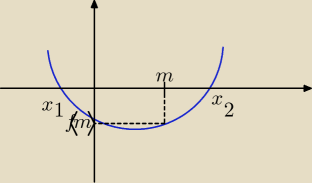
16 paź 15:20
t.: okej, dzięki

wyszło mi, że m∊(−
∞,(−5−
√17)/2)∪((−5+
√17)/2,+
∞), dobrze?
16 paź 15:22
t.: powie mi ktoś czy dobrze obliczyłam dziedzinę? bo taki dziwny wynik w sumie wyszedł.
16 paź 15:46
TOmek: x2−4(m+1)x+2m(m−1)=0
Δ=[−4(m+1)]2−4*2m(m−1)
Δ=[−4m−4]2−8m(m−1)
Δ=16m2+32m+16−8m2+8m=
8m2+40m+16
16 paź 16:00
t.: no też mi tak wyszło, ale ja skróciłam jeszcze przez 8 wszystko.
potem policzyłam deltę m, wyszło 17, no i na koniec policzyłam m1 i m2.
dobrze mi wyszło?
16 paź 16:02
TOmek: 8m2+40m+16>0
−m(m+6)<0
dla m ∊ (−∞,6) v (0,∞)
16 paź 16:11
t.: ale tak wychodzi z warunku f(m)<0
a jest jeszcze warunek, że Δ>0
16 paź 16:14
16 paź 16:15
t.: Godzi, tak mi właśnie wyszło.
czyli m∊(−∞,(− 5 + √17)/2) ∪ ((−5 + √17)/2, + ∞)
a z warunku f(m)<0 m∊(−∞,6) ∪ )o,+∞)
tylko nie wiem jaka jest część wspólna z tego?
16 paź 16:19
t.: *Godzio

16 paź 16:19
Godzio:
Oszacuj wartość tych wyrażeń i sprawdź czy są większe/mniejsze od 0 i 6, a część wspólna będzie
formalnością

Ale to akurat widać na oko
16 paź 16:22
t.: m∊(−∞,(−5−√17)/2)∪(0,+∞)
tak?
16 paź 16:25
Godzio: Tak
16 paź 16:28
t.: dzięki wielkie

16 paź 16:29
t.: mam jeszcze pytanie.
czy dla warunku f(m)<0
m∊(−∞,6)?
bo mi wychodzi, że do −6
16 paź 16:36
TOmek: f(m)=m2−4m(m+1)+2m(m−1)<0
m2−4m2−4m+2m2+2m<0
−m2−2m<0
−m(m+6)<0
(−∞,−6) v (0,∞)
16 paź 17:33
bigchungus : Big chungus
10 sty 20:31
10 sty 20:33

 wyszło mi, że m∊(−∞,(−5−√17)/2)∪((−5+√17)/2,+∞), dobrze?
wyszło mi, że m∊(−∞,(−5−√17)/2)∪((−5+√17)/2,+∞), dobrze?

 Ale to akurat widać na oko
Ale to akurat widać na oko
