całka podwójna Lachu: Całka podwójna Mam problem z całką podwójną, nie wiem gdzie robie błąd...

	xy2		x
∫∫ysin		dydx Obszar x=0, y=√π, y=
	2		2

	x
Obszar mi wyszedł 0≤x≤2√π 0≤y≤
	2

	xy2
Najpierw zrobiłem całkę przez podstawienie (		) a następnie po podstawieniu po y,
	2

wychodzi mi trudna całka...

Lachu: ..

Grześ: Już Pomogę

AS: Spróbuj podstawić y²/2 = t , wtedy 2y/2 dy = dt czyli ydy = dt

Lachu: ale nie lepiej sie pozbyć stałej x?

Grześ:

	x
Najpierw policzymy całke po y, dla √π≤y≤		, czyli:
	2

x
2

	xy2		xy2   cos   2		x3   cos   8		πx   cos   2
∫ ysin		dy = [−		] = −		+		,
	2		x		x		x

teraz: √π Liczymy po x, dla 0≤x≤2√π: 2√π

	x3   cos   8		πx   cos   2
∫ (−		+		) dx
	x		x

0 Pomyślę chwilkę i zaraz rozpisze całki

Grześ: o kurde.... z tej postaci to raczej nie ma szans policzyć całki... wyjdzie tak skomplikowana... musi być o wiele prostszy sposób na to zadanko.. hmm

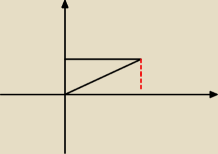
Lachu: chyba y zmieniają się od 0 do x/2, czy się myle?

Lachu: kurcze ja mam wątpliwość tylko co do obszaru czy dobrze zaznaczyłem...

Lachu: kurde chyba obszar źle zaznaczyłem, nie wiem czy y nie powinien się zmieniać (x/2 do √π)

Lachu: prosze o pomoc