awdawda ludwik: Rozwiąż równanie |x+1|³ −3|x+1|²≥0 mógłby ktoś to dla mnie rozwiązać?

ludwik:

ludwik: nikt nie potrafi mi pomóc ?

Dawid: Wg mnie: Rozpisujemy wartość bezwzględna:

	⎧	x+1 gdy x≥−1
|x+1| =	⎨
	⎩	−x−1 gdy x<−1

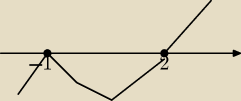
Zaczynamy od robienia w przedziałach a więc: 1. x≥−1 (x+1)³ −3(x+1)²≥0 x³+3x²+3x+1−3(x²+2x+1)≥0 x³+3x²+3x+1−3x²−6x−3≥0 x³−3x−2≥0 dla x=2 wielomian równa się zero a więc x³−3x−2 dzielimy przez x−2 i otrzymujemy (x−2)(x²+2x+1)≥0 zauważ że drugi nawias to wzór skróconego mnożenia a więc (x−2)(x+1)²≥0 Rysujemy linie rys wyzej gdzie otrzymujemy że x=−1 i x≥2 Obydwa wynika należa do założenia 1 a więc sa poprawne. 2 sposób analogiczne tylko w przedziale x<−1 (−x−1)³−3(−x−1)²≥0

Grześ: Pomagam

Grześ: robimy tak: |x+1|³−3|x+1|²≥0 |x+1|²(|x+1|−3)≥0, czyli |x+1|² zawsze jest nieujemne, czyli nie wpływa na wynik, czyli mozna pominąć: |x+1|−3≥0 |x+1|≥3 z własności: x+1≥3 ⋁ x+1≤−3 x≥2 ⋁ x≤−4 x∊(−∞,−4>U<2,+∞) Czy nie szybciej?