Ciągi Kasia: Ciągi − zadania Witajcie. Mam wkrótce sprawdzian z ciągów i chciałabym naprawdę dobrze wyćwiczyć zadania z tego działu, przejrzałam większość rzeczy, które są na tej stronie i chciałabym teraz sprawdzić się czy naprawdę to umiem. Z początku prosiłabym o jakieś proste zadania, a jak mi pójdzie dobrze to sukcesywnie co raz trudniejsze Poziom podstawowy! Z góry bardzo dziękuję

ICSP: mam zadania z ciągu ale jak chcesz mogę dać również z algebry abstrakcyjnej

Kasia: nie, nie, podziękuję jeszcze jestem w liceum więc nie rozkręcaj się i poproszę bardzo o jakieś zadanka z ciągów, ale proste z początku, bo czasami miałam problemy z zadankami z tego działu, a zależy mi bardzo żeby wszystko sobie uporządkować w głowie i nie mieć problemu później na sprawdzianie i na maturze oczywiście

ICSP: podstawa/rozszerzenie?

Kasia: podstawa

ICSP: to może na początek takie proste. w ciągu arytmetycznym dana jest różnica równa 5 oraz a₃ + a₅ = 30 oblicz a₄

Kasia: ok, to tak : r = 5 a₃ + a₅ = 30 rozpisuje drugie równanie w inny sposób : a₁ + 2r + a₁ + 4r = 30 a₁ + 2*5 + a₁+ 4 *5 = 30 a₁ + 10 + a₁ + 20 = 30 2a₁ = 0 / :2 a₁ = 0 a₄ = a₁ + 4r a₄ = 0 + 20 a₄ = 20 dobrze?

ICSP: a₄ = a₁ + 3r

Kasia: fakt, fakt! kurcze, takie głupstwo zrobić : ( ok, następne?

ICSP: a teraz następne. Oblicz a₄ w ciągu arytmetycznym jeśli a₃ + a₅ = 30

Kasia: i oczywiście a₄ = 15

ICSP: szybko

ICSP: tylko miałaś napisać a nie podać odpowiedź

Kasia: to zadanie już mi się nie podoba chwilka, spróbuję coś wymyślić ale da się na pewno zrobić ? xD

ICSP: tak

jacek: an=4n*(3/5)*{n−1}

Kasia: na pewno muszę ułożyć układ równań, żeby wyliczyć r i a₁ i wtedy bez problemu się wyliczy a₄ , tylko jakie drugie równanie.. ale jeszcze nie podpowiadaj, jak się poddam to dam znać

jacek: jest ciągiem geometrycznym

deskjet: Prosze bardzo niektore przepisze ze zbioru a ze dwa wymysle sam 1) Wykaz ze w ciagu arytmetycznym(a_n) o roznicy r

	2a1+(n−1)r
Sn=		*n
	2

2)Oblicz ile kazdy z nas mogł miec maksymalnie biologicznych praprapraprapraprzodków

	3+√15		3√5+4√3
3)sprawdz czy liczby: √3,		,		tworzą ciąg geometryczny
	2		2

4)Suma trzech liczb tworzących ciąg geometryczny jest rowna 19 a suma ich kwadratów jest rowna 133 jakie to liczby? 5)Trzy liczby ktorych iloczyn wynosi 64 tworzą ciąg geometryczny te same liczby tworzą ciąg arytmetyczny wyznacz te liczby 6)czy ciąg a_n=2ⁿ jest geometryczny?

	2n
7)czy ciąg an=		jest arytmetyczny?
	n+1

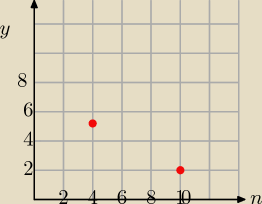
8) Na wykresie na gorze przedstawiłem ciąg a własciwie wykres i dwa jego punkty jest to ciąg arytmetyczny y=a_n uzasadnij ze jest to ciąg malejący Powodzenia

Kasia: przecież podał ICSP , że jest ciągiem arytmetycznym...

ICSP: on do innego zadania.

ICSP: moje zadanie brzmi: a₃ + a₅ = 30 oblicz a₄ jeżeli jest to ciąg arytmetyczny

jacek: pomocy sprawdź czy ciąg an=4n*(3/5)*{n−1} jest ciągiem geometrycznym z góry dziękuje za pomoc

krystek: Nie przeszkadzajcie Kasi i ICSP−owi

Kasia: aa.. Jacek załóż osobny wątek, bo robisz tutaj zamieszanie... ICSP, prosze o podpowiedz z drugim rownaniem, bo nic niestety nie wymyśle..

ICSP:

	3
4n *		* (n−1)
	5

ICSP: a jakie znasz wzory dla ciągu arytmetycznego?

Kasia: a_n = a₁ + (n−1) *r

	an −1 + an + 1
an =
	2

	a1+ an
Sn =		*n
	2

ale w pierwszym i ostatnim wzorze jest 'n' więc byłaby to kolejna, trzecia niewiadoma. aaa.. czyli z tym drugim faktycznie da się zrobić, to daj mi kilka minutek .

Kasia: tylko, że jest problem, bo podstawiając w drugim równaniu mi wychodzi 2a₁ + 6 r = 2a₁ + 6 r czyli nic mi to dalej nie da.. buuu

Kasia: no tak, skoro to jest to samo to nie dziwota, że wychodzi to samo, haha to chyba źle trafiłam ze wzorem

ICSP: w drugim wzorze z n wstaw 4 i zobacz co wyjdzie

Kasia: tzn z tym wzorem na sume początkowych wyrazów?

ICSP: drugi to średnia arytmetyczna.

Kasia: ale nie za bardzo rozumiem jak mam podstawić, tak :

	a3 − 1 + a5 +1
a4 =		?
	2

wtedy mam przecież już 3 niewiadome

ICSP: Skąd te jedynki ?

Kasia: to wzór wygląda tak:

	an−1 + an+1
an =		?
	2

w sumie wygląda tak samo, chodzi mi o to, że te jedynki są tak jakby na dole, w sensie, że są razem z 'n' , czyli n−1 i n+1 jeśli tak, to widocznie źle zapisałam sobie w zeszycie.

ICSP: a_n a_n−1 dla n = 4 a₄ a₄₋₁ = a₃

	a3 + a5
czyli a4 =
	2

Dokończ.

Kasia: aaaaaaaaaaaaaaaaaaaaaaaaaaaa a₃ + a₅ = 30

	a3 + a5
a4 =
	2

	30
a4 =
	2

a₄ = 15 takie proste, tylko trzeba wpaść na to ,że z tego wzoru trzeba skorzystać następne?

ICSP: na razie zajmij się tymi z 20:43. Ja muszę iść coś zjeść

Kasia: ok, smacznego

Kasia: 6 i 7 odpowiedz nie , tak mi sie wydaje a z reszta mam problem.. moge prosic o podpowiedzi do pozostałych

Kasia: a co do zadań z 'wykaż, że ' to chyba moge sobie je odpuścić, bo takich na lekcjach nie robiliśmy więc podejrzewam, że nie pojawią się na klasówce.

Mateusz: Niby tak ale ykazac 1 wzor jest bardzo prosto wręcz trywialnie 6 i 7 jak sie sprawdzało czy ciąg jest arytmetyzny czy geometryczny liczyło sie n+1 wyeraz i jezeli roznica albo iloraz ni zalezały od n to ciąg był rytmetyczny,czy geometryczny w przypadku ilorazu. 2) Skorzystaj z własnosci ciągu geometrycznego: an²=a_n−1*a_n+1 3) No to sprobujmy wipisac co nie co zaczynając od siebie Ja mama, tata babcia,druga babcia,drugi dziadek prababcia,pradziadek,druga prababcia,drugi pradziadek itd... zauwazmy ze liczby przodkow tworzą ciąg geometryczny o wyrazie a₁=8 i q=2 my szukamy wyrazu a₅ bo(praprapraprapra]] a₅ policzymy łatwo 4)kolejne wyrazy ciągu geometrycznego to a₁,a₂q,a₃q² a₁+a₂+a₃=19 trzeba rozwiązac układ rownan i wyznaczyc te liczby a₁+a₂q+a₃q²=19 a₁² +a₂q²,a₃q⁴=144 5) oznaczamy sobie te liczby jako np x,y,z ich iloczyn wynosi 74 a więc: x*y*z=64 tworzą ciąg geometryczny: korzystam więc z jego włąsnosci podanej w zadaniu 3 y²=x*z te liczby tworzą takze ciag arytmetyczny a więc korzystam z własnosci tego ciągu takiej ze roznica dowolnego wyrazu i wyrazu bezposrednio go poprzedzającego jest stała dla danego ciągu a więc: y−x=z−y jak zbierzemy to do kupy to mamy układ do rozwiązania: x*y*z=64 y²=x*z y−x=z−y 8)ciąg jest malejący gdy kazdy wyraz jest większy od następnego wyrazu

Mateusz: w 4) ma byc 133 a nie 144 pomyliłem się w 5) ich iloczyn wynosi 64 a nie 74

krystek: Na koniec sie włącze. Może to Kasi pomoże.Ale fajno,że chce się nauczyć a nie czeka na gotowce. Jeżeli a₃,a₄, a₅ tworzą ciąg arytmetyczny to różnica jest stała czyli a₅−a₄=a₄−a₃ stąd 2a₄=a₅+a₃

	a5+a3
to a4=
	2

Kasia: dzięki wielkie Mateusz ! Jestem Ci bardzo wdzięczna za pomoc zaraz po kolei sobie przeglądne i rozwiąże ile bym dała żeby to wszystko odrazu widzieć, ah

Mateusz: Nie trzeba nic dawać tylko nabrać wprawy a najlepiej sie to robi rozwiązując zadania tak jak ty podoba mi sie twoja postawa jest godna nasladowania

Kasia: i Tobie Krystek również dziękuję, myślę, że może mi się to przydać : ) już zabieram się do rozwiązywania

krystek: Spokojnej nocy

Kasia: zad. 3 nie chce mi się wypisywać wszystkich obliczeń po kolei, bo pewnie z 5 minut jak nic by mi to zajęło, w każdy razie w skrócie zrobiłam tak

3√5 + 4√3		3+ √15		3+√15
	:		=
2		2		√3

i później po wykonaniu dzielenia sprowadziłam oba ułamki do wspólnego mianownika i licznik nie wyszedł taki sam, więc odpowiedz : nie jest to ciąg geometryczny. zgadza się? : )

Mateusz: Niestety nie probuj dalej podpowiem ci ze

	3+√15		9+6√15+15		6√15+24		3(√15+4)
an2=(		)2=		=		=
	2		4		4		2

i teraz sprawdz czy iloczyn a_n−1*a_n+1 wynosi tyle samo co an²

Kasia: ale dlaczego nie wychodzi.. mając na przykład takie wyrazy ciągu 1, 2, 4 to żeby sprawdzic czy jest to ciąg geometryczny wystarczy podzielić wyraz od poprzedniego i wtedy 4 : 2 = 2:1 , więc dlaczego to co napisałam nie jest prawdą?

Kasia: czekam cierpliwie na odpowiedz reszte zadanek zrobie jutro, bo już mnie spanie bierze dobrej nocy wszystkim : )

marek: Ciąg geometryczny to ciąg gdzie dla trzech jego kolejnych wyrazów a,b,c jest spełniona zależność b²=ac a wiec w naszym wypadku 2²=4*1, dzielac kolejny wyraz przez poprzedni otrzymamy natomiast iloraz ciągu

krystek: I ja uparcie podpowiadam def ciągu geometrycznego a,b,c,sa kolejnymi wyrazami ciągu geom. gdy iloraz jest stały:

c		b
	=		i konsekwencja tej zależności jest:
b		a

b²=a*c

Kasia: czyli to co napisałam o 22:47 jest prawdą, tak?

Kasia: ICSP : widzę,że jesteś na forum, znajdziesz dziś też chwilkę żeby pomóc?

ICSP: jak tylko skończę sprawdzać czy a*b = 5^{log₅ a log₅ b} jest grupą to mogę pomóc

ICSP: dobra. Element naturalny i odwrotny policzę później. Mów którego zadania nie możesz zrobić?

Kasia: najpierw chciałabym rozwikłać problem, który wynikł wczoraj, z tym dzieleniem, jak to w końcu jest? bo na lekcji wyliczaliśmy za pomocą dzielenia, a tutaj Mateusz wziął to za błąd, więc już mam mętlik w głowie, jak to w końcu jest? chodzi o mój post z 22:47, ja twierdze, że to co napisałam jest prawdą..

ICSP: jeżeli a₁, a₂, a₃ tworzą ciąg geometryczny to

a2		a3
	=
a1		a2

a z tego wynika że : (a₂)² = a₃ * a₁ Jest to wyprowadzenie wzoru na średnia geometryczną z własności ciągu. Jeśli chodzi o twój przykład. Lewa strona jest zapisana poprawnie. Prawa już niestety nie.

Kasia: zgubiłam mianownik '2' poprawiając :

3√5+ 4√3		3+√15		3+√15
	:		=		: √3
2		2		2

ICSP: i teraz wymnażasz na krzyż i wychodzi ci to samo co by wyszło na początku z użyciem wzoru.

Kasia: wiem już jak to wyliczyć tylko niepotrzebnie wcześniej zgubiłam 2, a wiedziałam jak to zrobić, no cóż, będę bardziej ostrożna ok, ale mi jakoś łatwiej wyliczyć dzieląc niż pamiętając ten wzór zabieram się jeszcze za zadania powtórkowe ze szkoły, jeśli natrafię na jakiś problem to tutaj wrzuce

Kasia: już natrafiłam na pewien problem zadanie brzmi : Suma dwóch pierwszych wyrazów ciągu arytmetycznego równa się 27, suma dwóch ostatnich wyrazów wynosi 105, a siódmy wyraz jest równy 30. Znajdź pierwszy wyraz i liczbę wyrazów tego ciągu. zrobiłam układ równań a₁ + a₁ + r = 27 a₁ + 6r = 30 z tego wyliczyłam, że r = 3 i a₁ = 12 i teraz nie wiem jak wyliczyć liczbe wyrazów ciągu. Na coś jest mi dana informacja, ze suma dwoch ostatnich wyrazow wynosi 105. Pytanie moje brzmi, czy da się jakoś to policzyć nie wypisując po kolei wyrazów?

ICSP: a_n−1 + a_n = 2a_n−1 + r

Kasia: skąd ten wzór się wziął bo za bardzo nie rozumiem?

ICSP: taka zabawa a₅ = a₄ + r a₆ = a₅ + r a_n = a_n−1 + r a_n−1 + a_n = a_n−1 + a_n−1 + r = 2a_n−1 + r

Kasia: a co jeśli ktoś nie wpadnie na tą ' zabawę'? da się jakoś inaczej to zrobić czy pozostaje wypisywanie wyrazów po kolei, aż dwa ostatnie zsumowane dadzą 105?

ICSP: najpierw piszesz wzór na a_n a_n = a₁ + (n−1)r a_n = 12 + 3n − 3 = 3n + 9 w takim razie a_n−1 będzie o r mniejszy i równy 3n + 6 3n + 9 + 3n + 6 = tam ileś i rozwiązujesz. Jak i na to nie wpadniesz to wypisuj wyrazy

Kasia: aaaaa, ten drugi sposób mi się podoba dziękuję Ci ogromnie

Kasia: odświeżam wątek. Wyznacz rosnący ciąg geometryczny, wiedząc, że suma wyrazów skrajnych jest równa 34, iloczyn tych wyrazów 64, a suma wszystkich wyrazów ciągu wynosi 62. wypisuje dane : a₁ + a_n = 34

a1
	= 64
an

Sn = 62 wyliczam n

	34n
62 =
	2

124 = 34 n

	11
n = 102
	62

więc już coś tutaj dziwnego się dzieje, bo n raczej powinno być liczbą całkowitą, co nie? jak się za to zabrać? proszę o pomoc.

Patryk: ten iloczyn to chyba zle

Kasia: no tak, a₁ * a_n = 62

Kasia: hm, a jakby ukladem rownan wziac te dwie pierwsze dane i wyliczyc a₁ i a_n? da mi to coś? i co później?

Patryk: ja nie wiem co to są wyrazy skrajne ? w tym zadaniu nie pomogę

Kasia: skrajne to wydaje mi się, że to jest pierwszy wyraz i ostatni. Czy ktoś inny może mi pomóc?

Kasia: ponawiam