Zadanie maturalne
Karpiu: Dla chętnych
Dany jest ostrosłup prawidłowy trójkątny. Odległość spodka wysokości od krawędzi bocznej jest
równa 6. Wysokość ostrosłupa tworzy z wysokością ściany bocznej kąt o mierze 60 stopni. Oblicz
pole powierzchni bocznej tej bryły.
Dodam, że dzisiaj na lekcji nawet nauczycielka matematyki nie wiedziała, jak to zadanie zacząć,
ale się udało, wynik wyszedł poprawny. Ciekawe czy któryś z was da radę. Zapraszam

14 paź 15:28
krystek: | | a√3 | |
A gdzie pojawił sie problem? wiadomo,że h= |
| i wysokości dzielą się w stosunku |
| | 2 | |
14 paź 15:34
Bizon: ... czy Ty krystek zrozumiałeś zadanie? −

14 paź 15:44
krystek: Ale w czym problem −nie wiem?
14 paź 15:47
Bizon: no właśnie nie wiesz ...
14 paź 15:48
krystek: A skąd wiesz? Skąd, na podstawie czego taka Twoja pewnośc?
14 paź 15:55
krystek: A istnieje podobieństwo?
14 paź 15:57
Bizon:
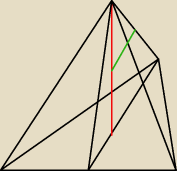
14 paź 15:59
krystek: A co to jest spodek wysokości?
14 paź 16:02
Bizon:
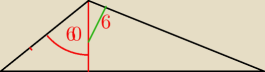
14 paź 16:04
krystek: Ja z Twoim rysunkiem nie zgadzam się .W zadaniu karpiu podał spodka wysokości ,a nie
środka
jak zaznaczasz.
14 paź 16:10
Bizon:
... no tak ... teraz można czepić się literki ... −

14 paź 16:13
krystek: Ale jest różnica między spodkiem a środkiem .Ale nie wiem czego Ty sie czepiałeś?
Na jakiej podstawie twierdzisz ,że nie wiem : Twój cytat:" no właśnie nie wiesz "
14 paź 16:19
Bizon:
niczego się nie czepiłem ... poprostu To co wypisałeś na początku to tylko prawda oczywista
mająca się nijak do "ścieżki" zadania ... a ton w jakim to napisałeś ...
14 paź 16:22
krystek: 
14 paź 16:25
Karpiu: Jak sobie radzicie? Widzę, że cisza, jak na razie

14 paź 17:46
Eta:
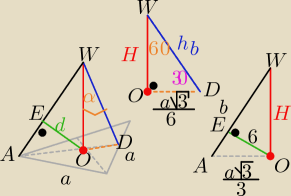
| | 1 | | a | |
z ΔODW mamy: H= |
| hb i hb= |
| ( sam dojdź do tego ) |
| | 2 | | 3 | |
zatem
| | a | |
z ΔAOW z tw. Pitagorasa b2= ........ => b= |
| √13 |
| | 6 | |
| | 1 | | a√3 | | a | |
porównując pola P(ΔAOW)= |
| * |
| * |
| =.... |
| | 2 | | 3 | | 6 | |
| | 1 | |
i P(ΔAOW) = |
| *b*6= 3b=..... |
| | 2 | |
| | a | |
otrzymasz: a=6√39 to hb= |
| = 2√39 |
| | 3 | |
P
b( ostr)= .................... =
702 [j2]

14 paź 19:16
karpiu: Wszystko się zgadza

14 paź 19:58
okoń : Całkiem trudne to zadanie nie rozumiem jeszcze jak z tych pól policzyliście a albo po prostu
robie jakiś błąd byłbym wdzięczny jakby ktoś rozpisał

2 maj 16:03










