.. pinokio: Stół Pinokia. Nos Pinokia mierzy 40 cm, nos jego żony 30 cm, a ich syna 20 cm. Pinokio chce ustawić w jadalni okrągły stół dostatecznie duży, aby wszyscy troje mogli usiąść wokół niego i obracać swobodnie głową bez ryzyka uderzenia się nosami. Zakłada się, że rzut prostopadły nasady każdego nosa znajduje się na krawędzi stołu lub poza stołem. Jaki powinien być, co najmniej, promień stołu? Wynik podać w centymetrach i zaokrąglić do najbliższej jednej dziesiątej.

pinokio: sprobuje ktos?

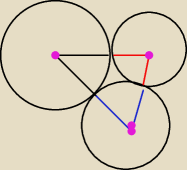
Student1roku: Ja bym to tak zrobił : ogólnie nasz stół będzie się opierał na tym zbudowanym trójkącie. Czarne okręgi wyznaczają obszar kreślenia końcem nosa obracającego się pinokia ( dowolnego, analigocznie mały okrąg to syn itd. ) . Gdy już mamy zbudowany trójkąt to pozostaje nam obliczyć promień okręgu opisanego na tym trójkącie. Obliczamy pole: P=√p(p−a)(p−b)(p−c) gdzie duże P to pole, małe p to połowa obwodu a,b,c boki trójkąta czyli np. a=20+30, b=20+40, c=30+40 I promień R=^abc_4p

Student1roku: Sorry w tym ostatnim wzorze jest P duże R=^abc_4P

pinokio: wydaje mi sie ze musza oni siedziec w rownych odstepach od siebie bo gdyby tak nie bylo to: (30+40):2=35 i juz mamy odpowiedz