w graniastosłupie prawidłowym sześciokątnym kąt nachylenia krótszej przekątnej mila: w graniastosłupie prawidłowym sześciokątnym kąt nachylenia krótszej przekątnej do płaszczyzny podstawy jest równy 30 stopni wiedząc że objętość graniastosłupa jest równa 12√3 oblicz długość krótszej przekątnej

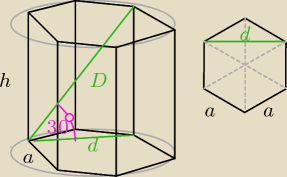
dero2005: pole podstawy P_p = ³₂a²√3 mniejsza przekątna podstawy d d = a√3 V = P_p*h = 12√3 stąd

	V		2V		2*12√3		8
h =		=		=		=		(*)
	Pp		3a2√3		3a2√3		a2

jednocześnie

h		√3		√3		a√3*√3
	= tg 30o =		→ h = d*		=		= a (**)
d		3		3		3

porównując obydwa wzory (*) i (**) obliczamy a

8
	= a
a2

a³ = 8 a = ³√8 = 2 teraz liczymy przekątną D z Pitagorasa D = √h² + d² h = a d = a√3 h² = a² = 2² = 4 d² = (a√3)² = 3a² = 3*2² = 12 D = √4 + 12 = √16 = 4 D = 4