współrzędne
sinusy: Hej, jak obliczyć współrzędne punktu jeżeli wiem że odcinek AC =6
leży na prostej y=x−2
i A=(−2;−4)?
zastosować wzór na długość odcinka? chyba tak nie wyjdzie bo są 2 niewiadome? zrobić zmienną
czy jak? Mam obliczyć współrzędne punktu C. proszę o podpowiedź
13 paź 20:21
sinusy: pomocy
13 paź 20:28
krystek: C=(x,y)=(x,x−1)
I tera wzór na dł odc
IACI=....
13 paź 20:33
sinusy: oki, ale skąd wzięła się zmiana współrzędnej w ten sposób?
13 paź 20:34
sinusy: obojętnie co mogę sobie tam podstawić? czy nie?
13 paź 20:35
krystek: punkt leży na prostej!
13 paź 20:35
Bizon: ułożyć układ dwóch równań (dwie niewiadome to współrzędne punktu C)
Jedno to o którym mówisz ... na długosć odcinka a drugie wynikające z faktu, że punkt C
leży na prostej (jego współrzędne spełniają równanie prostej)
13 paź 20:35
krystek: Masz wzór prostej y=x−2!
więc nie możesz sobie dowolnie wstawiać co chcesz!
13 paź 20:37
krystek: Bizon i zostaje jedna niewiadoma !
13 paź 20:38
sinusy: czyli to drugie równanie mogę ułożyć w ten sposób, że podstawie do wzoru wyznaczającego prostą
przechodzącą przez dwa punkty współrzędne punktu A, czyli do wzoru
(y−ya)(xb−xa)−(yb−ya)(x−xa)=0?
13 paź 20:40
Jolanta: Krystek a dlaczego w punkcie C y=x−1 ?
13 paź 20:40
krystek: Ponieważ punkt C leży na prostej (warunek podany w zadaniu)
13 paź 20:41
sinusy: Dobrze mówię czy nie bardzo?
13 paź 20:43
sinusy:
13 paź 20:44
krystek: Nie!
13 paź 20:45
Jolanta: prosta y=x−2
13 paź 20:46
krystek: IACI=√(xc−xa)2+(yc−ya)2
13 paź 20:47
sinusy: nie wychodzi mi

13 paź 20:51
sinusy: nom to wiem
pewnie rachunki żle , licze jeszcze raz
13 paź 20:51
Jolanta: Krystek proszę Cie wytłumacz dlaczego x−1 skoro y=x−2
13 paź 20:53
sinusy: rozumiem że wyznaczam np. y z tej prostej i podstawiam do wzoru na długość odcinka z czego
szukam jednej wspólrzednej punktu C, ale nadal nie wychodzi
13 paź 20:56
krystek:
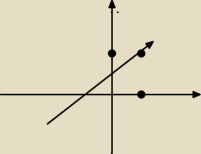
No włśnie dlatego!
13 paź 20:58
sinusy:
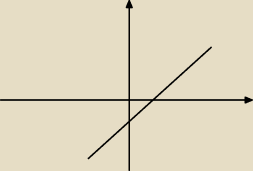
13 paź 21:00
krystek: Jeżeli punkt leży na prostej to ma współrzędne (x,y) a y przyjmuje postać z podanego wzoru x−2
i
koniec.
13 paź 21:00
Bizon: jaka niewiadoma zostaje Krystek?
dwa równania ....dwie niewiadome
13 paź 21:00
sinusy: prosta leży tak..
13 paź 21:00
sinusy: a myślę że punkt A ma −2;−4 poniewaz lezy na tej prostej i mysle ze tworzy z punktem B odcinek
rownolegly do ox
13 paź 21:02
krystek: Ale rys tłumaczyłam Jolancie.
IACI2=(xc+2)2+(yc+4)2
62=(xc+2)2+(xC−2+4)2 i licz
13 paź 21:07
Gustlik: C=(x, x−2)
A=(−2;−4)
Wektor AC→=C−A=[x+2, x−2+4]=[x+2, x+2]
|AC|=√(x+2)2+(x+2)2
√(x+2)2+(x+2)2=6 /()2
(x+2)2+(x+2)2=36 → dokończ...
13 paź 21:08
sinusy: no ale tam jak jest xc−2 podstawione to trzeba do kwadratu znowu podniesc caly nawias czyli
(xc−2)2
13 paź 21:11
sinusy: uhym z wektorów czyli jaki jest ogólny wzór na to?
13 paź 21:11
krystek: sinusy co Ty wymyślasz?
13 paź 21:16
sinusy: Dobra nie rozumiem, dzięki za pomoc
13 paź 21:21
krystek: Mówie Tobie wzór na długość odcinka jest taki sam jak długośc wektora .
13 paź 21:24
Jolanta: Sinusy jestes jeszcze ?
13 paź 21:30
krystek: Ale powiedz czego nie rozumiesz?
Np obl długośc odc AB gdy A(3,m) B(k,5)
IABI2=(k−3)2+(5−m)2
A my mieliśmy A(−2,−4) C(x,x−2) oraz podana była długośc odcinka AC=6 stąd
62=(x−(−2))2+(x−2−(−4))2 i czy teraz jasne?
13 paź 21:39

 No włśnie dlatego!
No włśnie dlatego!
