Pole trójkąta o danych współrzędnych jego wierzchołków. bez_pojęcia: Punkty A(−2;1), B(4;4) C(1;5) są wierzchołkami trójkąta. Oblicz pole trójkąta ABC.

Eta: → →

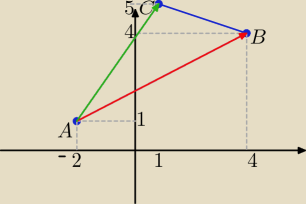
	1
P=		| det(AC, AB)| det −− wyznacznik pary wektorów zaczepionych
	2

w jednym punkcie → AB=[6,3] → → → det(AB, AC)= 6*4−3*3= 15 AC=[3,4] P= 7,5 [j²]

Gustlik: [P[Eta], brawo, to najlepszy sposób obliczania pola trójkata, ja go pokazuję na podstawach, bo w szkołach mało który nauczyciel pokazuje ten wzór. Przewaznie liczą długiośc podstawy, równanie prostej zawierającej podstawę oraz wysokość opuszczoną na tę podstawe i podstawiają

	1
do klasycznego wzoru P=		ah. Liczenia z pięć razy więcej. I tyle samo razy większe
	2

prawdopodobieństwo popełnienia błędu, czyli utraty punktów na maturze.

bez_pojęcia: dzięki!

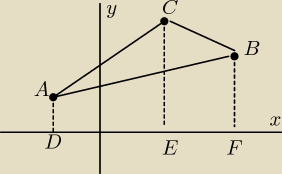
AS: PΔABC = P(trapezu ADCE) + P(trapezuCEFB) − P(trapezuADFB) Podstawami trapezu są wartości rzędnych odpowiednich punktów. Wysokościami trapezu różnice odciętych odpowiednich punktów np. dla trapezu ADCE podstawami będą yA i yC , wysokością xE − xD