Prawdopodobieństwo - niezależność zdarzeń Artek: W urnie są 3 kule białe i 2 czarne. losujemy dwukrotnie jedną kulę ze zwracaniem.Przyjmując oznaczenia : A − za drugim razem wyciągnięto kulę czarną B − za pierwszym razem wyciągnięto kulę białą, ustalić czy zdarzenia A i B są niezależne Bardzo proszę o pomoc, bo z prawdopodobieństwa jestem cienki

Gustlik: |Ω|=5*5=25 |A|=5*2=10 → P(A)=... |B|=3*5=15 → P(B)=... A∩B − za drugim razem wyciągnięto kulę czarną i za pierwszym razem wyciągnięto kulę białą, |A∩B|=3*2=6 → P(A∩B)=... Warunek niezależności zdarzeń: P(A∩B)=P(A)*P(B) Dokończ.

Artek: dziękuję bardzo

Artek: Jeszcze jedno zadanko mam proszę znów o pomoc w ramach możliwości Będę bardzoo wdzięczny W kartonie znajduję się 100 żarówek w tym 5 wadliwych. Z kartonu wyjęto 5 żarówek. Jakie jest prawdopodobieństwo, że : a) wszystkie wyciągnięte żarówki są dobre b) wśród wyjętych żarówek dokładnie 2 są wadliwe

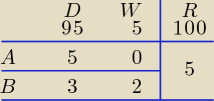
Bogdan: D − dobre, W − wadliwe, R − razem

	100 5		100*99*98*97*96
|Ω| =		=
			1*2*3*4*5

	95 5		5 0		95*94*93*92*91
|A| =		*		=		* 1
					1*2*3*4*5

	95 3		5 2		95*94*93		5*4
|B| =		*		=		*
					1*2*3		1*2

	|A|
P(A) =		= ...
	|Ω|

	|B|
P(B) =		= ...
	|Ω|