. Gruby: mam pytanie jak rysuje się wykresy takich funkcji? b)f(x)=| |x|−1| c) f(x)=|x−1|+1 e)f(x)=|x−1|+|x| f)f(x)=√x²−2x+1−|x| <− tutaj to mogę zapisać, że √x²−2x+1=|x−1| do b) napisali żeby rysować wykresy po kolei g(x)=|x| ; h(x)=|x|−1 i f(x)=|h(x)| no dobra, zrobie sobie ich tabelki dla tych samych x−ów tzn −1,0,1 g(x)=|x| ; h(x)=|x|−1 namalowałem odbiłem to co pod osią x−ów nad oś i o co chodzi dalej? Jak namalować wykres dla tej jednej funkcji f(x)=| |x|−1| ?

Gruby: precyzując do b) na razie mam wykresy 3 różnych funkcji, bo kazali najpierw narysować takie pomniejsze funkcje g(x)=|x| ; h(x)=|x|−1 i f(x)=|h(x)| ale nie wiem jak to połączyć w jeden wykres

ZKS: b) y = x ^{| |} → y = |x| ^{Tu→ = [0 ; −1]}→ y = |x| − 1| ^{| |} → y = ||x| − 1|.

Gruby: już się domyśliłem w b) to po prostu rysuje g(x)=|x| później im chodziło o to żeby przesunąć na osi y o 1 w dół i na końcu odbić to co pod osią w sumie to banalne,sorry za zaśmiecanie forum.

Tancerz: Godzio zaglądnij do postu mojego

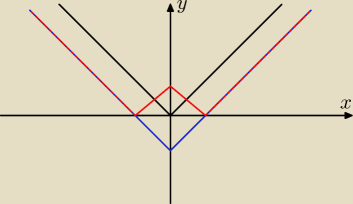ZKS: y = |x| y = |x| − 1 y = ||x| − 1|

Gruby: to mi wyszło dziękuje.Resztę już zrobię sobie sam.

Gruby: zrobiłem prawie wszystko, tylko jak zrobić, ostatni przykład ? f)f(x)=√x²−2x+1−|x|⇔f(x)=|x−1|−|x| nie chodzi o wykresy. Tylko o to co należy po kolei robić, żeby powyznaczać przedziały dla których należy odwrócić znak wartości bezwzględnej przy takich funkcjach jak ta f(x)=|x−1|−|x|. {1 dla x<0 powinno wyjść f(x)={−2x+1 dla x∊<0,1) {−1 dla x≥1 ale jak do tego dojść ?

Gruby: to nie jest trudne wiem, ale styczność miałem tylko z takimi przykładami gdzie była tylko jedna wartość bezwzględna. Wytłumaczy ktoś jeden przykładzik ?

ZKS: f(x) = √x² − 2x + 1 − |x| f(x) = |x − 1| − |x| dla x ∊ (−∞ ; 0) f(x) = −x + 1 + x f(x) = 1 dla x ∊ <0 ; 1) f(x) = −x + 1 − x f(x) = −2x + 1 dla x ∊ <1 ; ∞) f(x) = x − 1 − x f(x) = −1