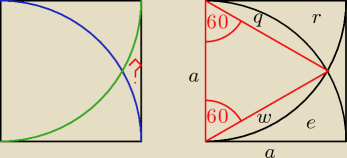
 Pytanko mam następujące. Czy mogę obliczyć pole fragmentu ze znakiem zapytania rysując trójkąt
równoboczny jak na drugim rysuneczku? Oznaczyłem poszczególne fragmenty jako q, w, r, e.
Kwadrat ma długość boku a. Te dwa przecinające się łuki mają promień długości a.
Moja propozycja rozwiązania jest następująca...
Pytanko mam następujące. Czy mogę obliczyć pole fragmentu ze znakiem zapytania rysując trójkąt
równoboczny jak na drugim rysuneczku? Oznaczyłem poszczególne fragmenty jako q, w, r, e.
Kwadrat ma długość boku a. Te dwa przecinające się łuki mają promień długości a.
Moja propozycja rozwiązania jest następująca...
| a2 √3 | ||
PΔ = | ||
| 4 |
| 60 | a2 √3 | πa2 | a2 √3 | |||||
Pq = Pw = | * πa2 − | = | − | = | ||||
| 360 | 4 | 6 | 4 |
| 2πa2 | 3a2 √3 | 2πa2 − 3a2 √3 | ||||
= | − | = | ||||
| 12 | 12 | 12 |
| 30 | 2πa2 − 3a2 √3 | |||
Pr = Pe = | * πa2 − | = | ||
| 360 | 12 |
| πa2 | 2πa2 − 3a2 √3 | πa2 − (2πa2 − 3a2 √3) | ||||
= | − | = | = | |||
| 12 | 12 | 12 |
| πa2 − 2πa2 + 3a2 √3 | −πa2 + 3a2 √3 | |||
= | = | |||
| 12 | 12 |
| a2 √3 | 2πa2 − 3a2 √3 | −πa2 + 3a2 √3 | ||||
P? = a2 − ( | + 2 * | + 2 * | ) = | |||
| 4 | 12 | 12 |
| 12a2 | 3a2 √3 | 4πa2 − 6a2 √3 | −2πa2 + 6a2 √3 | |||||
= | − ( | + | + | = | ||||
| 12 | 12 | 12 | 12 |
| 12a2 | 3a2 √3 + 4πa2 − 6a2 √3 −2πa2 + 6a2 √3 | |||
= | − | = | ||
| 12 | 12 |
| 12a2 − (3a2√3 + 2πa2) | 12a2 − 3a2 √3 + 2πa2 | |||
= | = | |||
| 12 | 12 |
| 12a2 − 3a2 √3 − 2πa2 | |
| 12 |