Wielościan wypukły madzia: Błagam o pomoc: Pewien wielościan wypukły ma jedną (tylko) ścianę 100-kątną. Z każdego wierzchołka tego wielościanu wychodzą co najmniej 4 krawędzie. Ile co najmniej ścian trójkątnych posiada ten wielościan?

adzia: i co?

Basia: jesteś pewna treści ? nie umiem sobie wyobrazić wielościanu, w którym z każdego wierzchołka wychodzą co najmniej 4 krawędzie

Basia: a nie przepraszam, oczywiście, że tak może być

Basia: nie, jednak nie potrafię sobie tego wyobrazić; jedyne wielościany z tą cechą jakie potrafię sobie wyobrazić to dwa ostrosłupy sklejone podstawami, ale wtedy wszystkie ściany są trójkatami

Bogdan: Wyobraźmy sobie bębenek, którego dolna i górna podstawa jest 100-kątem foremnym, a ściany boczne są trójkątami, wtedy z każdego wierzchołka wychodzą 4 krawędzie. Ścian bocznych trójkątnych jest 200. Taka bryła nazywa się półforemnym graniastosłupem 100-kątnym skręconym. A teraz do jednej z 100-kątnych podstaw bębenka przyklejmy ostrosłup prawidłowy 100-kątny. To jest właśnie ten wielościan wypukły, który ma jedną ścianę 100-kątną, 200 + 100 = 300 ścian trójkątnych.

Eta: Bogdanie! Jesteś niesamowity Dobranoc! ( pewnie przyśni mi się ten "bębenek"

b.: Hmm nie rozumiem do końca -- Bogdan podał przykład takiego wielościanu, ale czy nie ma innych, które mają mniej ścian trójkątnych?

Basia: nie ma, to jest absolutne minimum każdy inny będzie miał więcej ścian trójkatnych też to w końcu wczoraj wymyśliłam, ale nie miałam już siły napisać

madzia: Jesteście pewni rozwiązania tego zadania? Ja nadal nie jestem przekonana do niego

Bogdan: Jednak może być mniej trójkątów.

madzia: Czy ktoś ma jeszcze pomysł na to zadanie?

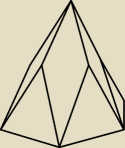
Marecki: Można stworzyć taki, który będzie miał 100 ścian trójkątnych. Weźmy ten 100− kąt i do każdej ściany przylepmy taki sam trójkąt równoramienny (tak jak w bębenku Bogdana), ale niech te trójkąty pochylają się nieco do środka bryły. Następnie zamiast wstawiać pomiędzy nie kolejne trójkąty, wstawmy czworokąty podobne do rombów (nie jestem pewny czy to będą romby), które będą stykać się na górze bokami i wierzchołkami. To tak jakbyśmy wzięli bębenek Bogdana, postawili na nim ostrosłup i odcinali kolejno płaszczyznami kawałki od wierzchołka ostrosłupa do wierzchołka 100− kąta.

Marecki: Właśnie zauważyłem, że ta bryła to po prostu ostrosłup, od którego odcinaliśmy wierzchołki przy podstawie.

Marecki: Przepraszam− korekta. Moja bryła nie spełnia warunku o co najmniej 4 krawędziach.