| −4 | ||
x2+2x+1≥ | ||
| x−2 |

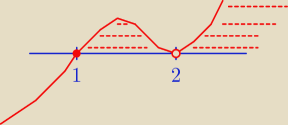 D = R − {2}
D = R − {2}
| 4 | ||
x2 + 2x + 1 ≥ − | ||
| x − 2 |
| (x2 + 2x + 1)(x − 2) | 4 | ||
+ | ≥ 0 | ||
| x − 2 | x − 2 |
| x3 − 2x2 + 2x2 − 4x + x − 2 + 4 | |
≥ 0 | |
| x − 2 |
| x3 − 3x + 2 | |
≥ 0 | |
| x − 2 |

| −4 | ||
x2+2x+1− | ≥0
| |
| x−2 |
| (X2+2x+1)(x−2)+4 | |
≥0 | |
| x−2 |
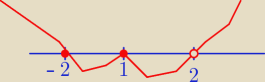 x3 − 3x + 2 = x3 − x − 2x + 2 = x(x2 − 1) − 2(x − 1) = x(x − 1)(x + 1) − 2(x − 1) =
= (x − 1)(x2 + x − 2)
Δ = 1 + 8 = 9, √Δ = 3, x1 = 1, x2 = − 2
Odp: x ∊ (−∞,−2> U (2,∞) U {1}
x3 − 3x + 2 = x3 − x − 2x + 2 = x(x2 − 1) − 2(x − 1) = x(x − 1)(x + 1) − 2(x − 1) =
= (x − 1)(x2 + x − 2)
Δ = 1 + 8 = 9, √Δ = 3, x1 = 1, x2 = − 2
Odp: x ∊ (−∞,−2> U (2,∞) U {1}
 dziękuję bardzo, teraz wiem gdzie popełniłam błąd.
dziękuję bardzo, teraz wiem gdzie popełniłam błąd.