Równanie z modułem wewnętrznym
Karolina__: Rozwiąz równanie:
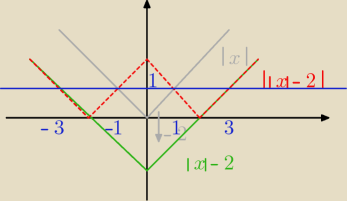
ǀǀxǀ−2ǀ=1
I. ǀxǀ−2 ≥0
ǀxǀ ≥2
x należących do <−2, +∞)
ǀxǀ−2=1
ǀxǀ= 3
x należy do {−3,3}
II. ǀxǀ−2<0
ǀxǀ<2
x należy do (−2,2)
−(ǀxǀ−2)=1
−ǀxǀ +2= 1
−ǀxǀ= −1 /(−1)
ǀxǀ=1
X należy do {−1, 1}
Odp. X należy do {−3, −1, 1, 3}.
Bardzo proszę powiedzcie czy dobre jest moje rozumowanie i wskażcie ewentualne błedy (sama
widzę, że niepotrzebnie piszę przedziały ponieważ jeśli x należy do przedziału <−2, +∞), to
nie zawiera się w nim −3 ale w rozwiązaniu jest. Nie rozumiem dlaczego tak się dzieje. Z góry
dziękuję za pomoc
Karolina,
odpowiedzi poprawne