Funkcje cyklometryczne
Godzio:
Obliczyć wartość wyrażenia:
Jakiś magiczny wzór albo coś ?
8 paź 01:12
Trivial: Pewnie że jest.

8 paź 01:13
Godzio:
Podpowiesz coś

?
8 paź 01:14
Trivial:
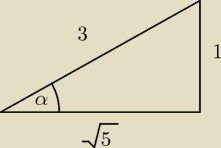
8 paź 01:16
Trivial: Tylko tylko, że śpię.
 √5
√5 jest oczywiście źle.
8 paź 01:17
Godzio:
Wtedy ...

możesz dokończyć bo robię zadania koledze i natrafiłem na takie cudo

te
| | 1 | |
podstawowe typu arccos |
| policzę, ale to jakieś dziwne |
| | 2 | |
8 paź 01:18
Trivial:
Najpierw poprawiamy ten wstrętny
√5 na to co powinno tam być, czyli 2
√2.
| | 1 | |
ctg(arcsin |
| ) = ctg(arcsin(sinα)) = ctgα = 2√2. |
| | 3 | |
8 paź 01:19
Godzio:
Ok kumam, dzięki

8 paź 01:22
Godzio: A jeszcze takie jedno,
Znaleźć funkcję odwrotną do f(x) = cosx , x ∊ [π,2π]
To wtedy f−1(x) = arccosx , x ∊ [−1,1] bo akurat dla π → = −1, a dla 2π →1 ?
8 paź 01:31
Trivial: Nie.
8 paź 01:33
Trivial: arccosx zwraca wartość z przedziału (zależnie od definicji) [0, π]. Ty chcesz mieć wartości z
przedziału [π, 2π]. Trzeba będzie dodać odpowiednią stałą i ewentualnie pomnożyć arcus przez
−1.
8 paź 01:35
Godzio:
A mógłbyś pokazać ten przykład, resztę zrobię analogicznie jakoś ?
8 paź 01:35
Trivial:
y = cosx
Przesuniemy wykres o π w lewo. Dzięki temu wstrzelimy się w standardowe wartości arcusa
cosinusa i nie będzie problemu.
y = cos(π+x−π) = −cos(x−π).
−y = cos(x−π) /arccos
arccos(−y) = x−π
x = arccos(−y) + π = π−arccos(y) +π = 2π−arccos(y) = f
−1(y).
Chyba dobrze, bo trochę śpię.

8 paź 01:49
Godzio:
Dobra wszystko jasne, po raz kolejny dzięki

8 paź 01:51
Trivial: 
8 paź 01:54
Godzio:
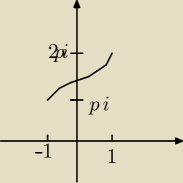
Tak na szybko, wykres tak będzie wyglądać ?
8 paź 02:05
b.: tak. swoją drogą, z wykresu można szybko odczytać, czy dobrze się policzyło (odbijasz kawałek
wykresu y=cosx względem prostej y=x (kawałek odp. x∊[π,2π]), a potem patrzysz, co trzeba
zrobić z wykresem arccos, żeby dostać Twój wykres)
8 paź 09:39

 ?
?
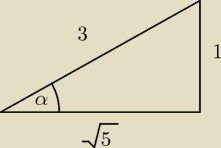
 √5 jest oczywiście źle.
√5 jest oczywiście źle.
 możesz dokończyć bo robię zadania koledze i natrafiłem na takie cudo
możesz dokończyć bo robię zadania koledze i natrafiłem na takie cudo  te
te




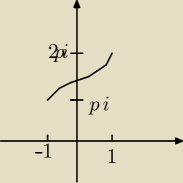 Tak na szybko, wykres tak będzie wyglądać ?
Tak na szybko, wykres tak będzie wyglądać ?