.
Michał: dana jest funkcja f(x)=|3x−6|+x+4 naszkicowac wykres funkcji f i rozwiazac nierownosc f(x)≤8
oonee: wykres.
robisz dwa przedziały(wynikające z modułu)
jeden gdy moduł przyjmuje wartości mniejsze od zera drugi gdy moduł przyjmuje wartości większe
równe zero
x≥2 => |3x−6| = 3x+6
x<2 => |3x−6| = −3x+6
szkicujesz wykres dla obu przedziałów (pilnuj zgodności rozwiązań z dziedziną przedziału)
nierówność tak samo, dwa przedziały dla |3x−6|+x−4≤0 (przerzuciłem już tą ósemke)
jeśli nie wiesz o co mi chodzi to dokładniej opisze

Eta:
dla x ≥0 f(x)= 3x−6+x+4 = 4x−2
dla x <0 f(x)= −3x+6 +x+4 = −2x+10
{ 4x− 2 dla x≥0
f(x)={
{ −2x+10 dla x <0
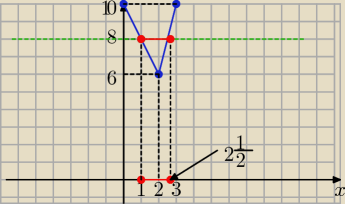
część wykresu f(x)= 4x−2 dla x≥2
dla x=2 f(2)= 4*2−2=6 , (2,6)
dla x=3 f(3) = 4*3−2=10 , (3,10)
podobnie druga część wykresu dla x<2 ( 1, 8), (0,10)
f(x) ≤8 => 4x−2 ≤8 i −2x+10≤ 8
x ≤2,5 i x ≥ 1
odp:
x€<1; 2,5>

 dla x ≥0 f(x)= 3x−6+x+4 = 4x−2
dla x <0 f(x)= −3x+6 +x+4 = −2x+10
{ 4x− 2 dla x≥0
f(x)={
{ −2x+10 dla x <0
część wykresu f(x)= 4x−2 dla x≥2
dla x=2 f(2)= 4*2−2=6 , (2,6)
dla x=3 f(3) = 4*3−2=10 , (3,10)
podobnie druga część wykresu dla x<2 ( 1, 8), (0,10)
f(x) ≤8 => 4x−2 ≤8 i −2x+10≤ 8
x ≤2,5 i x ≥ 1
odp:
x€<1; 2,5>
dla x ≥0 f(x)= 3x−6+x+4 = 4x−2
dla x <0 f(x)= −3x+6 +x+4 = −2x+10
{ 4x− 2 dla x≥0
f(x)={
{ −2x+10 dla x <0
część wykresu f(x)= 4x−2 dla x≥2
dla x=2 f(2)= 4*2−2=6 , (2,6)
dla x=3 f(3) = 4*3−2=10 , (3,10)
podobnie druga część wykresu dla x<2 ( 1, 8), (0,10)
f(x) ≤8 => 4x−2 ≤8 i −2x+10≤ 8
x ≤2,5 i x ≥ 1
odp:
x€<1; 2,5>