liczba stanowi sumy liczb

zadania thompson ;):

	x		x		1
B.		−		+1=		(x+6)
	2		3		6

	5
C. 1−2x+		=4
	3

	1		1		x
D. x−		− x+		=−
	4		2		4

	x		x		1
B.		−		+1=		(x+6) / *6
	2		3		6

3x−2x+6=x+6 0=0 ⇒ rownanie tozsamosciowe

	5
C. 1−2x+		=4 /*3
	3

3−6x+5=12 6x=−4

	2
x=−
	3

	1		1		x
D.x−		− x+		=−		/*4
	4		2		4

4x−1−4x+2=−x x=−1

6 paź 19:56

xddd: Liczba r stanowi 10% sumy liczb r i p, 20% liczby t jest o 6 mniejsze od v, Liczba o 15% większa od x jest z razy mniejsza od y.

6 paź 20:03

da: asddsasad

6 paź 20:14

Dla Ciebie xD: i co robisz ?

6 paź 20:14

thompson ;): Liczba sprzężona do liczby z=x+iy? Napisz.

6 paź 20:26

Dla Ciebie xD: pisze xd

6 paź 20:30

Dla Ciebie xD: liczbe sprzezona do z=x+iy

6 paź 20:38

Dla Ciebie xD: z=x−iy

6 paź 20:44

thompson ;): z₁ = 2 − 3i ; z₂ = 5 + i ; z₃ = −4i ; z₄ = 5i − 6 Na razie tyle.

6 paź 20:46

Dla Ciebie xD: z₁ "_" =2+3i z₂ "_"= 5−i z₃ "_"= 4i z₄"_" = −6−5i

6 paź 20:50

thompson ;): emotka

6 paź 20:51

thompson ;): Wyznacz Re(z) i Im(z) liczby zespolonej. z₁ = 12 + 14i ; z₂ = 5 − 2i ; z₃ = 2(−3i +2) − 4i Na razie tyle.

6 paź 20:54

Dla Ciebie xD: Re(z)=12 Im(z)=14 Re(z)=5 Im(z)=2 Re(z)=4 Im(z)=10

6 paź 20:59

thompson ;): Im(z₂) = −2 Im(z₃) = −10 Reszta emotka

6 paź 21:01

thompson ;): Dane są następujące liczby zespolone: a = 5 − 6i ; b = i + 3 − 2i ; c = i ; d = 2 + 0i − 2i − 2 + 2i Wykonaj działania a + b = a − b = a * b = a − (b + c) + a * d =

a
	=
d

b
	=
a

6 paź 21:05

Dla Ciebie xD: a+b= 8−5i a−b=2−7i

6 paź 21:13

Dla Ciebie xD: (5−6i)*(3+i)= 15+5i−18i − ? =

6 paź 21:14

thompson ;): a + b = 5 − 6i + 3 − i = 8 − 7i a − b = 5 − 6i − (3 − i) = 2 − 5i

6 paź 21:15

thompson ;): (5 − 6i)(3 + i) = 15 + 5i − 18i − 6i² = dokończ!

6 paź 21:16

thompson ;): Tam powinno być (5 − 6i)(3 − i) źle obliczyłeś popraw!

6 paź 21:19

Dla Ciebie xD: a*b = 15−11i+6i²

6 paź 21:27

Dla Ciebie xD: a − (b + c) + a * d = 2−6i−0i²

6 paź 21:31

thompson ;): Ile to jest i² = ?

6 paź 21:31

Dla Ciebie xD: i *i

6 paź 21:32

Dla Ciebie xD: 5−18i

6 paź 21:33

thompson ;): i² = −1 a więc popraw

6 paź 21:33

Dla Ciebie xD: 14−11i

6 paź 21:34

thompson ;): Ale które to jest?

6 paź 21:35

Dla Ciebie xD: a * b =

6 paź 21:39

thompson ;): Źle

6 paź 21:39

thompson ;): a * b = (5 − 6i)(3 − i) = 15 − 5i − 18i + 6i² = dokończ

6 paź 21:42

Dla Ciebie xD: a − (b + c) + a * d = 2−6i

6 paź 21:43

Dla Ciebie xD: a * b = (5 − 6i)(3 − i) = 15 − 5i − 18i +6i² = 9 − 23i

6 paź 21:44

thompson ;): emotka

6 paź 21:44

Dla Ciebie xD:

3−i
	=
5−6i

(3−i)(5+6i)

(5−6i)(5+6i)

6 paź 21:57

thompson ;):

15 + 18i − 5i − 6i²
	= dokończ
25 + 36

6 paź 22:00

Dla Ciebie xD:

15+13i−6
	=
61

9−13i

61

6 paź 22:03

thompson ;):

15 + 13i + 6
	= ?
61

6 paź 22:08

thompson ;): Modułem liczby zespolonej z = x + iy nazywamy liczbę: |z| = √x² + y²

6 paź 22:24

thompson ;): Policzyć moduły liczb zespolonych: a = 5 + 6i b = i + 3 − 4i c = 3i d = 3 + 0i − 3i − 3 + 3i

6 paź 22:27

Dla Ciebie xD: a=√61 b=3√2 c=3 d=0

6 paź 22:32

thompson ;): |a| = √61 tak samo dla b ; c i d

6 paź 22:34

Dla Ciebie xD: a=√61 v √−61 b=−3√2 v −3√2 c=3 v c=−3 d=0

6 paź 22:37

thompson ;): Moduł liczby zespolonej jest liczba rzeczywistą czyli nie może być √−coś

6 paź 22:40

Dla Ciebie xD: okej rozumiet

6 paź 22:40

thompson ;): Liczbę zespoloną z = x + iy można zapisać w postaci trygonometrycznej:

	x		y
z = x + iy = \|z\|(cosφ + isinφ) gdzie \|z\| = √x² + y² i cosφ =		i sinφ =
	\|z\|		\|z\|

6 paź 22:45

thompson ;): Przedstawić następujące liczby zespolone w postaci trygonometrycznej: a = 4 − 4i b = −√2 + i√2 c = −√2 − i√6

6 paź 22:47

Dla Ciebie xD: |z|* √2/ 2 + i −√2/2

6 paź 22:54

Dla Ciebie xD:

	√2		−√2
z\|*		+ i
	2		2

6 paź 22:55

thompson ;): Liczę moduł |z| = √4² + (−4)² = √2 * 4² = 4√2

	4		1		√2
cosφ =		=		=		(I i IV ćwiartka)
	4√2		√2		2

	7
⇒ φ =		π
	4

	−4		−1		√2
sinφ =		=		= −		(III i IV ćwiartka)
	4√2		√2		2

	7		7
z = 4√2(cos		π + isin		π)
	4		4

6 paź 23:03

Dla Ciebie xD: rysunek

6 paź 23:08

Dla Ciebie xD: rysunek

6 paź 23:11

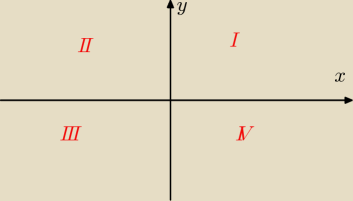
thompson ;): rysunek

6 paź 23:11

thompson ;): I ćwiartka − sinus + ; cosinus + II ćwiartka − sinus + ; cosinus − III ćwiartka − sinus − ; cosinus − IV ćwiartka − sinus − ; cosinus +

6 paź 23:15

Dla Ciebie xD: rysunek

6 paź 23:16

Dla Ciebie xD: U √2/2

6 paź 23:20

Dla Ciebie xD:

√2

2

6 paź 23:20

Dla Ciebie xD:

	√2
sinφ =
	2

	−√2
cosφ=
	2

6 paź 23:34

thompson ;): emotka

6 paź 23:35

Dla Ciebie xD:

3pi

4

6 paź 23:36

thompson ;): emotka

6 paź 23:37

Dla Ciebie xD:

	3π		3π
z = 2(cos		+ isin		)
	4		4

6 paź 23:38

thompson ;): emotka

6 paź 23:38

Dla Ciebie xD:

	π		π
z = 2√2(cos		+ i * sin		)
	3		3

6 paź 23:43

Dla Ciebie xD: ℛ

6 paź 23:45

thompson ;): Źle

6 paź 23:52

Dla Ciebie xD:

	4π
z = 2√2(cos		+ isin^4π₃)
	3

7 paź 00:01

thompson ;): Masz np:

	√3		1
sinα =		i cosα = −
	2		2

Teraz napisz która to ćwiartka i nie patrz na kartkę

7 paź 00:03

Dla Ciebie xD: druga

7 paź 00:05

thompson ;): emotka

Czyli wiem że jest to II ćwiartka teraz bierzesz obojętne czy

	√3		1
sinα =		czy cosα = −
	2		2

	√3
Ile to jest sinα =		w stopniach?
	2

7 paź 00:09

thompson ;): rysunek

7 paź 00:28

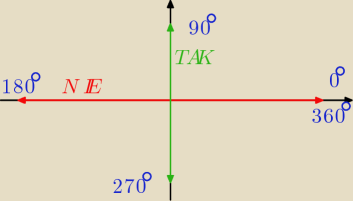
thompson ;): TAK czyli przechodzimy na kofunkcje np: sin(90^o − α) = cosα sin(90^o + α) = cosα sin(270^o − α) = −cosα (−) bo sinus w III ćwiartce jest ujemny sin(270^o + α) = −cosα (−) bo sinus w IV ćwiartce jest ujemny

7 paź 00:33

thompson ;): NIE czyli nie przechodzimy na kofunkcje np: cos(180 − α) = −cosα (−) bo cosinus w II ćwiartce jest ujemny cos(180 + α) = −cosα (−) bo cosinus w III ćwiartce jest ujemny cos(360 − α) =cosα cos(360 + α) = cosα

7 paź 00:41

thompson ;): Użyj wzorów redukcyjnych: cos(210^o) = sin(240^o) = sin(300^o) = cos(330^o) =

7 paź 00:44

thompson ;): cos(210^o) = cos(180^o + 30^o) = −cos30^o bo cosinus w III ćwiartce ujemny

7 paź 00:54

Dla Ciebie xD: sin(240^o) = sin (180^o + 60^o) = sin 60^o

7 paź 01:01

Dla Ciebie xD: −sin 60^o

7 paź 01:04

thompson ;): emotka

7 paź 01:05

Dla Ciebie xD: sin (360^o − 60^o) = −sin 60^o sin(270^o +60^o) = − sin 60^o

7 paź 01:08

thompson ;): 2π = 360^o

3
	π = 270^o
2

π = 180^o

π
	= 90⁰
2

7 paź 01:22

thompson ;):

	π		1		π		√3
sin		= sin30^o =		cos		= cos30^o =
	6		2		6		2

	π		√2		π		√2
sin		= sin45^o =		cos		= cos45^o =
	4		2		4		2

	π		√3		π		1
sin		= sin60^o =		cos		= cos60^o =
	3		2		3		2

7 paź 01:26

thompson ;): Oblicz:

	2
sin		π =
	3

	3
cos		π =
	4

	5
cos		π =
	4

	5
sin		π =
	3

7 paź 01:28

thompson ;):

	2		4		3		1		π		π
sin		π = sin(		π) = sin(		π +		π) = sin(		+		) = ?
	3		6		6		6		2		6

7 paź 01:32

Jack: użyj wzorów redukcyjnych: https://matematykaszkolna.pl/strona/430.html (PS wystarczyło napisać sin(2/3π)=sin(π− 1/3π)=... )

7 paź 01:40