...
Hermiona.: Proszę o pomoc bo doszłam do pewnego momentu i nie wiem co zrobić dalej

Oblicz promien kuli wpisanej w ostroslup prawidlowy czworokatny,jezeli jego podstawa jest
sciana szescianu o krawedzi dlugosci 8,a wierzcholkiem punkt przeciecia przekatnych szescianu.
6 paź 17:57
Hermiona.: halo

6 paź 18:23
Hermiona.: 
prosze o pomoc..
6 paź 18:50
ICSP: ale sweet

6 paź 18:52
ICSP: chociaż powiem szczerze ze odczytanie planu zajęć na UMCS jest trudniejsze.
6 paź 18:56
6 paź 18:58
ICSP: Masz odpowiedzi?
Wypadłem z wprawy i mogę głupoty gadać. Mi wyszło 4(√2−1)
6 paź 18:59
Hermiona.: tak

tak ma wyjsc
Prosze cie rozpisz mi to bo kurwicy dostane....
6 paź 19:01
Hermiona.: i jak mozesz to ten trojkat narysuj..
6 paź 19:02
ICSP:
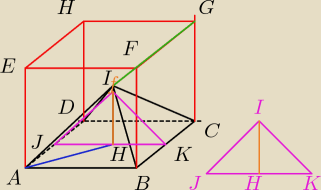
Niestety troszkę źle narysowałem i krawędź górna pokrywa się troszkę z przekątną.
Najpierw analiza trójkąta AHI (i jest punktem przecięcia się przekątnych.
|AH| = 4
√2
|AI| = 4
√3
|HI| liczysz z twierdzenia Pitagorasa i wychodzi 4.
|JK| = 8 czyli |HJ| = 4 = |HK|
|IJ| = |IK| = 4
√2
∡HJI = ∡HKI = 45
o
Z sumy miar katów w trójkącie wyliczamy trzeci kat: JIK = 90
o
Teraz proste równanie:
4
√2 − r + 4
√2 − r = 8 ⇔ −2r = −8
√2 + 8 ⇔ r = 4(
√2−1)
6 paź 19:11
Hermiona.: Prosze Cie ICSP pomoz mi z tym zadaniem...
6 paź 19:11
Hermiona.: Jejku,ubóstwiam Cie

6 paź 19:12
Hermiona.: A mozesz mi doradzic co tu zrobic? Bo jak oblicze H i to tez mi te r zoastaje i nie wiem czy z
katow czy jak.. Bo tam kat byl z wlasnosci a tu nie wiadomo...
Oblicz pole powierzchni kuli opisanej na ostroslupie prawidlowym czworokatnym jezeli krawedz
podstawy jest rowna 10 a krawedz boczna 5√3
6 paź 19:15
ICSP: Daj odpowiedź.
6 paź 19:20
Hermiona.: 225π
6 paź 19:22
Trivial: Czy to jest czterowymiarowy rysunek?

6 paź 19:22
ICSP: ... jak już tu jesteś to zrób drugie zadanie

6 paź 19:26
Hermiona.: ICSP powiedz mi dlaczego tak napisales ost rownanie... skad sie wziela ta zaleznoasc?
6 paź 19:29
Hermiona.: dlaczego to jest rowne 8?
6 paź 19:29
Hermiona.: przeciez r to 1/2 dlg podstawy czyli 4... bo jest oparte na srednicy
6 paź 19:31
Trivial: ICSP, nie mam ochoty na geometrię.

6 paź 19:32
ICSP:
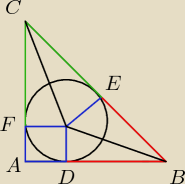
|AD| = |AF|
|FC| = |CE|
|BD| = |BE|
|BC| = |AB| − |AD| + |CA| − |FA|
6 paź 19:33
ICSP: jak to nie masz ochoty na geometrię? Już zaczynasz robić to zadanko

W tej chwili

6 paź 19:34
Trivial: Nie.

6 paź 19:35
6 paź 19:35
ICSP: Tak

Jak nie to chociaż zrób rysunek bo nie wiem jak to policzyć. Tzn. nie wiem nawet co policzyć bo
policzyć to nie problem.
6 paź 19:36
Trivial: nie.

6 paź 19:44
ICSP: Też nie wiesz

Trzeba na
Etę poczekać

Ona nas zawsze ratuje

6 paź 19:46
Trivial: Nie wiem czy wiem, czy nie wiem. Nie próbowałem i nie spróbuję.

6 paź 19:47
Eta:
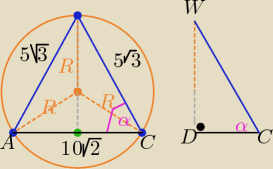
AC −−− przekątna kwadratu
|AC|= 10
√2
|DW|
2= (5
√3)
2−(5
√2)
2
| | 5 | | √3 | |
|DW|= 5 oraz sinα= |
| = |
| |
| | 5√3 | | 3 | |
ze wzoru sinusów :
| | 5√3 | |
|
| =2R => ....... R=7,5 |
| | sinα | |
P
k= 4πR
2=...... = 225 π [j
2]
6 paź 20:25
Eta:
dla
ICSP 

6 paź 20:28
ICSP: dla
Ety 

6 paź 20:28
Eta:

6 paź 20:29
Hermiona.: Dziękuję

6 paź 20:45
Hermiona.: Ale ie rozumiem skad sie wzielo ze wzoru sinusów :
5√3/sinα= 2R
z jakiego wzoru sinusow?
6 paź 20:51
6 paź 20:53
Eta:
2 sposób
| | a*b*c | | 10√2*5 | |
R= |
| a=10√5 , b= c=5√3 P= |
| = 25√2 |
| | 4P | | 2 | |
| | 10√2*5√3*5√3 | |
R= |
| =... = 7,5 |
| | 100√2 | |
6 paź 20:57
Hermiona.: ah tak...
Naprawde bardzo Ci dziekuje.
6 paź 20:57
Eta:
Na zdrowie

6 paź 20:58
Eta:
2 sposób jest prostszy

6 paź 20:59
Iza: Mi się tam podoba 1

6 paź 22:11
Iza: Akurat sie sklada ze to samo zadanie rozwiazywalam i akurat znalazlam i przydalo sie

6 paź 22:12
Eta:

6 paź 22:29
 Oblicz promien kuli wpisanej w ostroslup prawidlowy czworokatny,jezeli jego podstawa jest
sciana szescianu o krawedzi dlugosci 8,a wierzcholkiem punkt przeciecia przekatnych szescianu.
Oblicz promien kuli wpisanej w ostroslup prawidlowy czworokatny,jezeli jego podstawa jest
sciana szescianu o krawedzi dlugosci 8,a wierzcholkiem punkt przeciecia przekatnych szescianu.

 prosze o pomoc..
prosze o pomoc..




 tak ma wyjsc
Prosze cie rozpisz mi to bo kurwicy dostane....
tak ma wyjsc
Prosze cie rozpisz mi to bo kurwicy dostane....
 Niestety troszkę źle narysowałem i krawędź górna pokrywa się troszkę z przekątną.
Najpierw analiza trójkąta AHI (i jest punktem przecięcia się przekątnych.
|AH| = 4√2
|AI| = 4√3
|HI| liczysz z twierdzenia Pitagorasa i wychodzi 4.
|JK| = 8 czyli |HJ| = 4 = |HK|
|IJ| = |IK| = 4√2
∡HJI = ∡HKI = 45o
Z sumy miar katów w trójkącie wyliczamy trzeci kat: JIK = 90o
Teraz proste równanie:
4√2 − r + 4√2 − r = 8 ⇔ −2r = −8√2 + 8 ⇔ r = 4(√2−1)
Niestety troszkę źle narysowałem i krawędź górna pokrywa się troszkę z przekątną.
Najpierw analiza trójkąta AHI (i jest punktem przecięcia się przekątnych.
|AH| = 4√2
|AI| = 4√3
|HI| liczysz z twierdzenia Pitagorasa i wychodzi 4.
|JK| = 8 czyli |HJ| = 4 = |HK|
|IJ| = |IK| = 4√2
∡HJI = ∡HKI = 45o
Z sumy miar katów w trójkącie wyliczamy trzeci kat: JIK = 90o
Teraz proste równanie:
4√2 − r + 4√2 − r = 8 ⇔ −2r = −8√2 + 8 ⇔ r = 4(√2−1)




 |AD| = |AF|
|FC| = |CE|
|BD| = |BE|
|BC| = |AB| − |AD| + |CA| − |FA|
|AD| = |AF|
|FC| = |CE|
|BD| = |BE|
|BC| = |AB| − |AD| + |CA| − |FA|
 W tej chwili
W tej chwili




 Jak nie to chociaż zrób rysunek bo nie wiem jak to policzyć. Tzn. nie wiem nawet co policzyć bo
policzyć to nie problem.
Jak nie to chociaż zrób rysunek bo nie wiem jak to policzyć. Tzn. nie wiem nawet co policzyć bo
policzyć to nie problem.

 Trzeba na Etę poczekać
Trzeba na Etę poczekać Ona nas zawsze ratuje
Ona nas zawsze ratuje

 AC −−− przekątna kwadratu
|AC|= 10√2
|DW|2= (5√3)2−(5√2)2
AC −−− przekątna kwadratu
|AC|= 10√2
|DW|2= (5√3)2−(5√2)2










