PROblem TOmek: rumpek mam dla Ciebie 'zadanko prośbe' bo robiłem je juz 3 razy i wydaje mi się ,ze jest zła odpowiedź w ksiązce. Zadanie z geom. analitycznej. Masz czas by zrobić sobie na kartce i podać wynik?

rumpek: daj to lookne jak będę w stanie zrobić bo dzisiaj coś nie pracuje na najwyższych obrotach xD

TOmek: w równoramiennym trójkącie prostokątnym punkt C=(3,−1) jest wierzchołkiem kąta prostego. Przeciwprostokątna trójkąta zawiera sie w prostej 3x−y+2=0. Wyznacz pozostałe wierzchołki trójkąta.

TOmek: juz wiem gdzie mam błąd, omg... oo

TOmek: głupiś tyś tomku : (

rumpek: i jaki masz wynik ? bo Δ to mam hardcore

	48		108
10x2 −		x −		= 0
	5		10

TOmek:

	3		19		9		17
(		,		) , (−		,−		)
	9		5		5		5

szczerzepowiedziawszy jeszcze nie mogę dojśc do prawidłowego wyniku ... ale staram sie

Trivial: Tam gdzieś wychodzi Δ?

TOmek:

	3		19
(		,		) tam błąd ...
	5		5

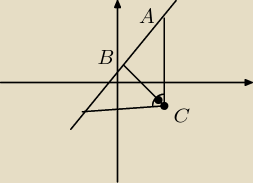
TOmek: y=3x+2 liczę prostą prostopadłą

	1
y=−		x
	3

	1
liczę ich punkt przeciecia "B"=(−		,1)
	3

	40
liczę |BC|2=
	9

|BA|=|BC| A=(x,3x+2) więc 40/9=(x+1/3)²+(3x+1)² x=−1

	1
x=
	3

rumpek: ja wpierw pouczę się historii zrobię zadanie z matmy a potem to zadanie pomęczę bo na pewno będzie układ równań:

	6		2		144
(x +		)2 + (y −		)2 =
	10		10		10

y = 3x + 2 3 razy liczyłem i ten sam układ otrzymuje xD

Trivial: Ja mam teorię jak 'łatwo' zrobić to zadanie. Ale łatwe pewnie okaże się trudne.

Trivial: Jaka jest prawidłowa odpowiedź?

TOmek: pokaz

TOmek:

	3		19		9		17
(		,		) , (−		, −		)
	5		5		5		5

rumpek: w sumie można też by zrobić inaczej, że: |AS| = |BS|, gdzie A i B leżą właśnie na tej prostej y = 3x + 2 wtedy ładnie do potęgi podnosimy a S to punkt przecięcia

rumpek: gdzie S to:

	1
−		x = 3x + 2
	3

−10x = 6 / : − 10

	6
x = −
	10

	2
y =
	10

rumpek: przecież ładnie wychodzi <sciana> widać, że jestem chory xD zaraz napisze

TOmek: http://www.wolframalpha.com/input/?i=%28-3%2F5-3%29%5E2%2B%281%2F5%2B1%29%5E2%3D%28-3%2F5-x%29%5E2%2B%281%2F5-3x-2%29%5E2 wyszło

TOmek: wyszło , amen

rumpek: tak jak pisałem rozwiązać układ równań:

	6		2		144
(x +		)2 + (y −		)2 =
	10		10		10

y = 3x + 2

	6		18		144
(x +		)2 + (3x +		)2 =
	10		10		10

	6		36		54		324		144
x2 +		x +		+ 9x2 +		x +		−		= 0
	5		100		5		100		10

	60		360		144
10x2 +		x +		−		= 0
	5		100		10

	60		36		144
10x2 +		x +		−		= 0
	5		10		10

	60		108
10x2 +		x −		= 0
	5		10

	60		108		3600		3600 + 10800
Δ = (		)2 − (−		* 4 * 10) =		+ 432 =		=
	5		10		25		25

	14400		120
=		⇒ √Δ =
	25		5

	60   120   − −   5   5		180   −   5		36		9
x1 =		=		= −		= −
	20		20		20		5

	60   120   − +   5   5		60		3
x2 =		= U{		{20} =
	20		5		5

więc już masz prawie zrobione teraz tylko y obliczyć tamtym drugim sposobem też powinno wyjść co napisałem

TOmek: fajowe ułamki, oby takich nie było na maturze, bo o błąd łatwo..

TOmek: no jak ładnie wyszło

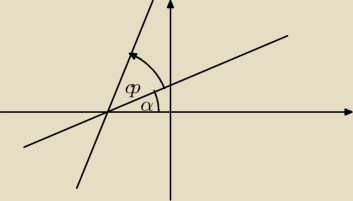
Trivial: Najpierw wyprowadzimy wzór na obrót prostej o kąt. Tak naprawdę interesuje nas tylko współczynnik kierunkowy tej prostej (ozn. a'). Wiemy, że: a = tgα Chcemy tą prostą obrócić o kąt φ. Możemy zapisać, że: a' = tg(α+φ). Szybkie przypomnienie wyprowadzenia wzoru na tangens sumy:

	sin(x+y)		sinxcosy + sinycosx
tg(x+y) =		=		=
	cos(x+y)		cosxcosy−sinxsiny

	sinx   siny   + cosx   cosy		tgx+tgy
=1		=		.
	sinx   siny   1− *   cosx   cosy		1−tgxtgy

(1) Dzielimy licznik i mianownik przez cosxcosy Zatem:

	tgα+tgφ		a+tgφ
a' =		=		.
	1−tgαtgφ		1−a*tgφ

Odnośnie zadania: C = (3,−1) Skoro trójkąt ABC jest równoramienny, to wystarczy obrócić prostą, którą dają w zadaniu o odpowiednie kąty: 45^o (ozn. a⁺) i −45^o (czyli 45^o w przeciwnym kierunku, ozn. a⁻). 3x−y+2 = 0 ⇔ 3x−y = −2 y = 3x+2 a = 3 Dla 45^o:

	a+tg(45o)		3+1
a+ =		=		= −2.
	1−a*tg(45o)		1−3

Prosta k⁺ przechodzi przez punkt C, a więc... −1 = 3*(−2) + b b = 5 k⁺: y = −2x + 5 ⇔ 2x+y = 5 Dla −45^o:

	a+tg(−45o)		3−1		1
a− =		=		=		.
	1−a*tg(−45o)		1+3		2

Prosta k⁻ przechodzi przez punkt C, a więc...

	1
−1 = 3*		+ b
	2

	5
b = −
	2

	1		5
k−: y =		x −		⇔ x − 2y = 5
	2		2

Aby znaleźć punkty wystarczy rozwiązać dwa układy równań:

⎧	2x+y = 5
⎩	3x−y = −2

oraz:

⎧	x−2y = 5
⎩	3x−y = −2

A miało być tak prosto. Odpowiedź się zgadza.

Trivial: Można zrobić to zdecydowanie prościej na wektorach i macierzach, ale to nie ten poziom.

TOmek: dokładnie, nie ten poziom

Trivial: Ale rachunki proste.

Trivial: Hmm, dopiero teraz zauważyłem, że ta różowa trójka w środku tworzy ciekawą kompozycję z resztą.