geometria gość: Działkę w kształcie trójkąta ABC o bokach AB = 34 m, BC =52m, CA =50 m, podzielono na dwie części prostą DE, równoległą do boku AB, oddaloną od niego o 20 m. Ile metrów bieżących siatki potrzeba na ogrodzenie każdej z działek? Przyjmujemy, że ogrodzimy je oddzielnie.

Michał:

nick: tak

aaa:

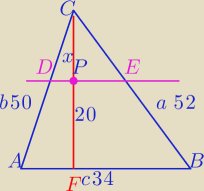
Mila: h=FC Obliczamy h, aby skorzystać z podobieństwa trójkątów 1) P_Δ=√p*Pp−a)*(p−b)*(p−c)

	34+52+50
p=		=68
	2

P_Δ=√68*18*34*16=√34*2*18*34*16=34*6*4=34*24

	1
PΔ=		*c*h
	2

1
	*34*h=34*24
2

1
	*h=24
2

h=48 x=|PC|=48−20=28 ΔDEC∼ΔABC⇔

	28		7
k=		=		skala podobieństwa
	48		12

	7		7*17
|DE|=		*34=		=..
	12		6

	7		7*13
|CE|=		*52=		=..
	12		3

|BE|=52−|CE|=...

	7		7*25
|CD|=		*50=
	12		6

dokończ rachunki

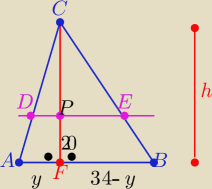Eta: 2 sposób ( bez wzoru Herona) Z tw, Pitagorasa : h²=50²−y² i h²=52²−(34−y)² to: 2500−y²=2704− 34²+68y−y² ⇒ 68y=952 ⇒ y=14 to h= √50²−14²= 48 i |PC|= 48−20= 28 i dalej .......... jak podała Mila